Rozwiązanie
Funkcja zapisana jest w postaci kanonicznej \(f(x)=a(x-p)^2+q\). Możemy więc zauważyć, że parametr \(m\) jest równy współrzędnej \(q\) wierzchołka paraboli.
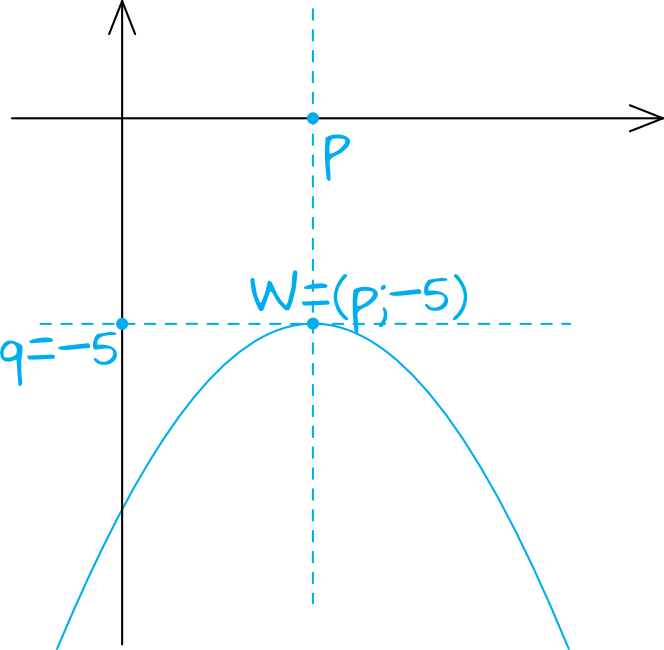
Z własności funkcji kwadratowych wynika, że funkcja przyjmuje największą lub najmniejszą wartość w swoim wierzchołku. Nasza funkcja ma ramiona paraboli skierowane do dołu (bowiem współczynnik \(a\) jest ujemny), czyli w wierzchołku będzie przyjmowana największa wartość tej funkcji. Ze zbioru wartości wynika, że największą wartością funkcji jest \(-5\), czyli że \(q=-5\). To oznacza, że tym samym \(m=-5\).