Zbiorem rozwiązań nierówności \(x(x+6)\lt0\) jest:
\((-6,0)\)
\((0,6)\)
\((-\infty,-6)\cup(0,+\infty)\)
\((-\infty,0)\cup(6,+\infty)\)
Rozwiązanie:
Krok 1. Wyznaczenie miejsc zerowych wielomianu.
Aby obliczyć miejsca zerowe musimy przyrównać \(x(x+6)\) do zera. Wielomian mamy podany w postaci iloczynowej, więc aby był on równy zero to któryś z czynników musi powodować jego „zerowanie”, zatem:
$$x(x+6)=0 \\
x=0 \quad\lor\quad x+6=0 \\
x=0 \quad\lor\quad x=-6$$
Krok 2. Szkicowanie wykresu paraboli.
Ramiona paraboli będą na pewno skierowane do góry, bo po wymnożeniu czynników otrzymalibyśmy dodatnią wartość współczynnika \(a\). Zaznaczamy na osi obliczone przed chwilą miejsca zerowe i odczytujemy rozwiązanie naszej nierówności. Kropki przy miejscach zerowych będą niezamalowane, bo w nierówności wystąpił znak \(\lt\).
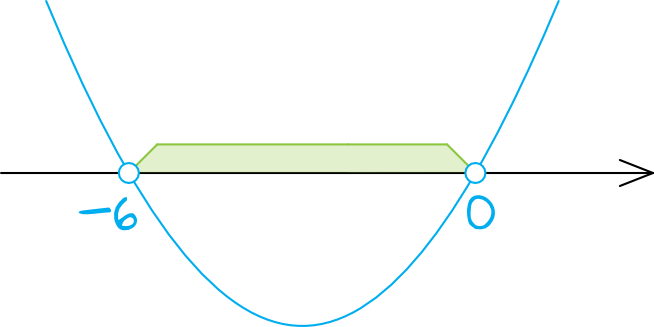
Interesują nas wartości mniejsze od zera, tak więc zbiorem rozwiązań tej nierówności jest przedział \(x\in(-6,0)\).
Odpowiedź:
A. \((-6,0)\)

