Rozwiązanie
Krok 1. Ułożenie nierówności kwadratowej.
Chcemy się dowiedzieć kiedy wartości funkcji \(f(x)\) są większe od wartości funkcji \(g(x)\), czyli chcemy sprawdzić kiedy:
$$f(x)\gt g(x) \\
-4x^2+x+5\gt-4x+6$$
Przenosząc teraz wyrazy na lewą stronę otrzymamy następującą sytuację:
$$-4x^2+5x-1\gt0$$
Powstała nam więc klasyczna nierówność kwadratowa, którą teraz musimy rozwiązać.
Krok 2. Obliczenie miejsc zerowych wielomianu.
Rozwiązywanie nierówności zaczniemy od wyznaczenia miejsc zerowych. Musimy więc sprawdzić kiedy \(-4x^2+5x-1\) jest równe \(0\). Z pomocą przyjdzie nam tutaj oczywiście niezawodna delta:
Współczynniki: \(a=-4,\;b=5,\;c=-1\)
$$Δ=b^2-4ac=5^2-4\cdot(-4)\cdot(-1)=25-16=9 \\
\sqrt{Δ}=\sqrt{9}=3$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-5-3}{2\cdot(-4)}=\frac{-8}{-8}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-5+3}{2\cdot(-4)}=\frac{-2}{-8}=\frac{1}{4}$$
Krok 3. Szkicowanie wykresu paraboli.
Współczynnik kierunkowy \(a\) jest ujemny, a to oznacza, że parabola będzie mieć ramiona skierowane do dołu. Zaznaczamy więc na osi wyznaczone miejsca zerowe \(x=1\) oraz \(x=\frac{1}{4}\) (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\gt\)) i rysujemy parabolę:
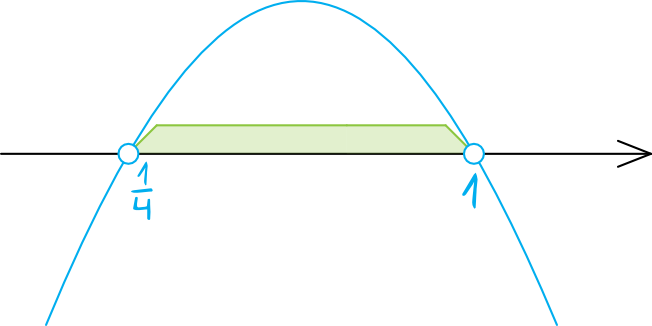
Krok 4. Odczytanie rozwiązania.
Interesują nas wyniki większe od zera, zatem patrzymy się na to co znalazło się nad osią. Ze szkicu paraboli wynika, że w takiej sytuacji rozwiązaniem tej nierówności jest przedział:
$$x\in\left(\frac{1}{4};1\right)$$