Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
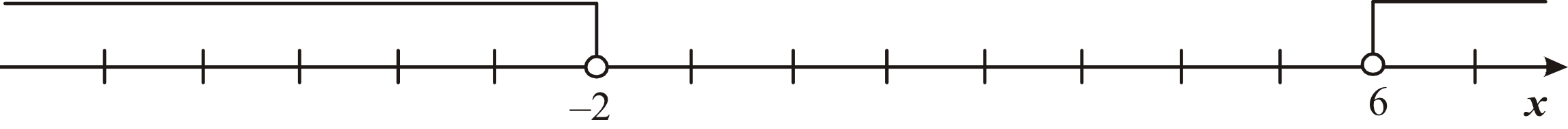
\(|x-2|\gt4\)
\(|x-2|\lt4\)
\(|x-4|\lt2\)
\(|x-4|\gt2\)
Rozwiązanie:
Zadanie to można rozwiązać obliczając każdą z nierówności podaną w odpowiedziach. Jeśli chcemy obliczyć to w sposób matematyczny, to możemy skorzystać z interpretacji geometrycznej zbioru rozwiązań nierówności. Na początek musimy wyznaczyć środek odcinka o końcach w punkcie \(-2\) oraz \(6\), a będzie to:
$$a=\frac{-2+6}{2}=\frac{4}{2}=2$$
Wyznaczony punkt \(a=2\) jest odległy od punktów końcowych (\(-2\) oraz \(6\)) o cztery jednostki. Skoro przedziały idą do plus/minus nieskończoności to zaznaczony zbiór jest zbiorem liczb odległych od punktu \(a=2\) o ponad \(4\) jednostki. Stąd też poszukiwaną nierównością jest \(|x-2|\gt4\).
Odpowiedź:
A. \(|x-2|\gt4\)

