Co to znaczy, że figury są podobne?
Na matematyce mówimy, że figury są podobne tylko wtedy, gdy spełnione zostaną dwa warunki jednocześnie:
· miary kątów jednej figury są takie same jak miary kątów figury drugiej;
· stosunki długości odpowiadających sobie boków jednej i drugiej figury są jednakowe (mówiąc wprost – każdy bok pierwszej figury musi być tyle samo razy większy lub mniejszy co drugiej figury).
Spójrzmy na poniższy rysunek z dwoma trapezami:
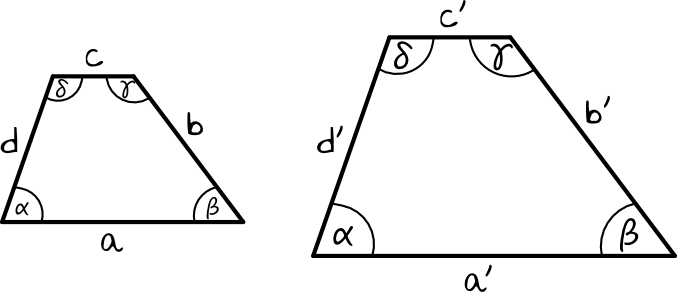
Aby te dwa trapezy można było uznać za podobne, to muszą mieć one te same miary kątów (widzimy, że w tym przypadku kąty są faktycznie tej samej miary), a miedzy bokami tych figur musiałaby zajść następująca zależność:
$$\frac{a’}{a}=\frac{b’}{b}=\frac{c’}{c}=\frac{d’}{d}$$
Podchodząc do tematu bardziej praktycznie, moglibyśmy powiedzieć, że przykładowo kwadrat o boku \(2cm\) oraz kwadrat o boku \(6cm\) to figury podobne, bo obydwie figury mają jednakowe kąty i każdy bok większego kwadratu jest \(3\) razy dłuższy od boku mniejszego kwadratu. A czy kwadrat o boku \(2cm\) i romb (który nie jest kwadratem) o boku \(6cm\) będą figurami podobnymi? Niestety nie będą, bo o ile faktycznie każdy bok rombu jest \(3\) razy większy od kwadratu, o tyle te figury nie będą miały jednakowych kątów.
Figura podstawowa i figura podobna
Kiedy podawaliśmy sobie przykład z kwadratami o bokach \(2cm\) oraz \(6cm\), to powiedzieliśmy, że ten większy kwadrat ma wszystkie boki \(3\) razy dłuższe. Jednak do sprawy można też podejść inaczej i moglibyśmy powiedzieć, że kwadrat o bokach \(2cm\) jest \(3\) razy mniejszy od dużego kwadratu. Obydwa podejścia są jak najbardziej słuszne, ale w bardziej rozbudowanych zadaniach często ten punkt odniesienia będzie niezwykle istotny. Ot chociażby za chwilę będziemy mówić o skali podobieństwa i wtedy kluczowe będzie ustalenie co do czego odnosimy.
Z tego też względu, aby uniknąć nieporozumień, często jedną figurę nazywamy „figurą podstawową”, a drugą, która jest do niej podobna, nazywamy „figurą podobną”. O tym która figura jest podstawowa, a która podobna, decydujemy samodzielnie, to i tak jest tylko umowne podejście. Nazewnictwo figur bardzo często będzie wynikać wprost z kontekstu zadania. Jeżeli przykładowo będziemy mieć informację, że „trapez \(PQRS\) jest podobny do trapezu \(ABCD\)”, to wtedy wyraźnie widzimy, że trapez \(ABCD\) jest figurą podstawową, a trapez \(PQRS\) będzie figurą do niego podobną.
Stosowanie tych pojęć nie jest obowiązkowe, ale znacząco ułatwia to późniejsze zrozumienie podobieństwa różnych figur.
Skala podobieństwa
Skalę podobieństwa oznaczamy symbolem \(k\) i za jej pomocą określamy stosunek długości odpowiadających sobie boków. Mówiąc bardziej obrazowo – skala podobieństwa informuje nas o tym, ile razy większa/mniejsza jest figura podobna względem figury podstawowej. Przykładowo:
· skala \(k=3\) oznacza, że figura podobna ma wszystkie odpowiadające boki \(3\) razy dłuższe od figury podstawowej;
· skala \(k=\frac{1}{3}\) oznacza, że figura podobna ma wszystkie odpowiadające boki \(3\) razy krótsze od figury podstawowej.
Chcąc obliczyć skalę podobieństwa musimy podzielić długość boku figury podobnej przez odpowiadający bok figury podstawowej. Spójrzmy na poniższy przykład.
Rozwiązanie:
Możemy przyjąć, że trójkąt \(ABC\) to nasza figura podstawowa, a trójkąt \(XYZ\) jest figurą podobną. Aby obliczyć skalę podobieństwa musimy długość boku trójkąta podobnego podzielić przez długość boku trójkąta podstawowego. W takiej sytuacji skala podobieństwa będzie równa:
$$k=\frac{20cm}{5cm} \\
k=4$$
Skala podobieństwa to \(k=4\), czyli możemy powiedzieć, że trójkąt \(XYZ\) ma wymiary \(4\) razy większe od trójkąta \(ABC\).
Tak na marginesie – oczywiście moglibyśmy przyjąć, że to ten duży trójkąt \(XYZ\) jest figurą podstawową, a trójkąt \(ABC\) figurą podobną. Wtedy skala podobieństwa byłaby równa:
$$k=\frac{5cm}{20cm} \\
k=\frac{1}{4}$$
To także byłaby dobra skala podobieństwa, tylko po prostu mamy tutaj inny punkt odniesienia. W przyszłych zadaniach już nie będziemy wyliczać tej skali dwukrotnie, ale warto pamiętać o tym, że jeśli będziesz wyliczać taką skalę i wyjdzie Ci wynik odwrotny, to jest to jak najbardziej możliwa sytuacja. Ważne jest tylko to, by w bardziej rozbudowanych zadaniach być konsekwentnym i stosownie później wyliczać potrzebne rzeczy.
Bardzo często skala podobieństwa będzie jednym z elementów potrzebnych do rozwiązania zadania. Jednym z takich najbardziej typowych zastosowań tej skali są zadania w których musimy wyznaczyć długość jakiegoś boku figury.
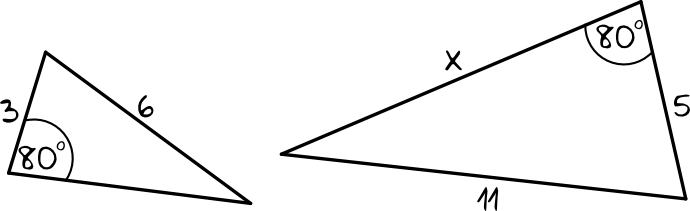
Rozwiązanie:
Aby wyznaczyć długość boku \(x\), musimy najpierw wyznaczyć skalę podobieństwa – będziemy wtedy wiedzieć, ile razy większy lub mniejszy jest nasz drugi trójkąt.
Aby wyznaczyć skalę podobieństwa musimy do obliczeń wziąć parę odpowiadających sobie boków. W jednym i drugim trójkącie znamy długość boku, który leży przy kącie o mierze \(80°\) i to jest ten krótszy bok (ważne, żeby się tutaj nie pomylić). Jeżeli więc przyjmiemy, że ten pierwszy trójkąt jest figurą podstawową, a drugi figurą podobną, to:
$$k=\frac{5}{3}$$
Wiemy już, że każdy odpowiadający bok figury podobnej jest \(\frac{5}{3}\) razy większy od figury podstawowej. Skoro tak, to poszukiwany bok \(x\) będzie \(\frac{5}{3}\) razy większy od boku o długości \(6\), zatem:
$$x=\frac{5}{3}\cdot6 \\
x=\frac{30}{3}=10$$
Pola figur podobnych
Skala podobieństwa przyda nam się także do obliczania pola powierzchni figur podobnych. Okazuje się, że stosunek pól powierzchni figur podobnych jest równy kwadratowi skali podobieństwa. Obrazowo rzecz ujmując, jeśli dana figura jest podobna do figury podstawowej w skali podobieństwa \(k\), to pole powierzchni figury podobnej będzie \(k^2\) razy większe od figury podstawowej.
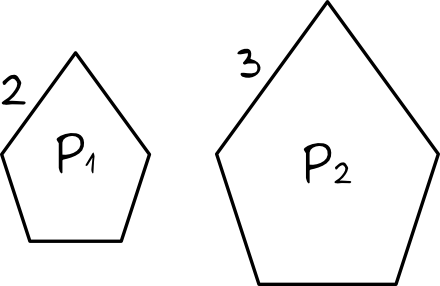
Rozwiązanie:
Rozwiązywanie zadania musimy zacząć od obliczenia skali podobieństwa. Bazując na długościach boków odpowiadających, możemy zapisać, że:
$$k=\frac{3}{2} \\
k=1,5$$
Wyszło nam więc, że druga figura ma wymiary \(1,5\) razy większe od figury pierwszej.
Aby wyznaczyć pole figury podobnej nie musimy stosować żadnych wzorów na pole. Pole powierzchni figury podobnej będzie \(k^2\) razy większe od pola figury podstawowej, czyli w naszym przypadku widzimy, że pole \(P_{2}\) powinno być \(2,25\) razy większe od pola \(P_{1}\), bo \(1,5^2=2,25\). Matematycznie całość moglibyśmy rozpisać w następujący sposób:
$$P_{2}=k^2\cdot P_{1} \\
P_{2}=1,5^2\cdot7 \\
P_{2}=2,25\cdot7 \\
P_{2}=15,75$$
Rozwiązanie:
Na podstawie informacji z treści zadania możemy przyjąć, że duży trapez o polu powierzchni \(104cm^2\) jest figurą podstawową, a mały trapez o polu \(26cm^2\) będzie figurą podobną. Z własności pól powierzchni figur podobnych wiemy, że stosunek pól powierzchni jest równy \(k^2\), czyli moglibyśmy zapisać, że:
$$k^2=\frac{26cm^2}{104cm^2} \\
k^2=\frac{1}{4} \\
k=\frac{1}{2} \quad\lor\quad k=-\frac{1}{2}$$
Skala podobieństwa musi być liczbą dodatnią, stąd też zostaje nam \(k=\frac{1}{2}\). Mówiąc bardzo obrazowo, wszystkie boki figury podobnej będą miały \(2\) razy mniejszą długość, czyli tym samym obwód tego mniejszego trapezu będzie tym samym dwukrotnie mniejszy. Matematycznie moglibyśmy zapisać, że:
$$Obw_{2}=k\cdot Obw_{1} \\
Obw_{2}=\frac{1}{2}\cdot22cm \\
Obw_{2}=11cm$$
Zobacz także inne tematy związane z podobieństwem figur:
