Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować ten trójkąt, zaznaczając na nim wszystkie informacje z treści zadania:
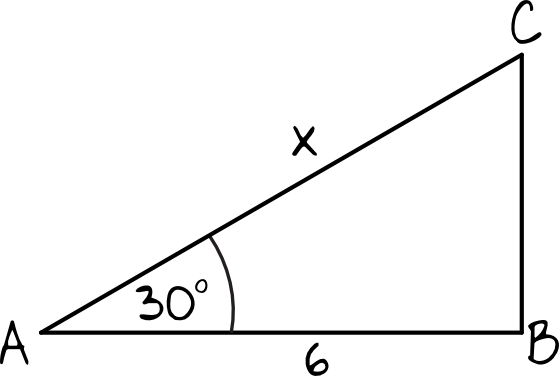
Tworząc rysunek należy pamiętać, że mniejszy kąt ostry trójkąta prostokątnego leży przy dłuższej przyprostokątnej.
Krok 2. Obliczenie długości przeciwprostokątnej.
Korzystając z funkcji cosinus możemy teraz zapisać, że:
$$cos30°=\frac{6}{x} \\
\frac{\sqrt{3}}{2}=\frac{6}{x}$$
Mnożąc na krzyż otrzymujemy:
$$\sqrt{3}x=12 \quad:\sqrt{3} \\
x=\frac{12}{\sqrt{3}} \\
x=\frac{12\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \\
x=\frac{12\sqrt{3}}{3} \\
x=4\sqrt{3}$$