Pole trójkąta - Matematyka

W tym temacie omówimy sobie to w jaki sposób obliczyć pole trójkąta, na co należy zwracać uwagę przy zadaniach z trójkątami oraz poznamy różne wzory na pole trójkąta, począwszy od tych podstawowych, a kończąc na bardzo zaawansowanych.

Wzór na pole trójkąta:
$$P=\frac{1}{2}ah$$
gdzie:
$P$ – pole trójkąta
$a$ – długość boku trójkąta
$h$ – wysokość trójkąta opuszczona na ten bok

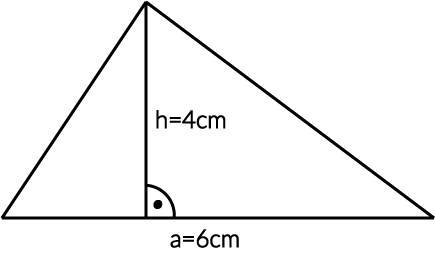
Przykład 1. Chcemy policzyć pole powierzchni powyższego trójkąta. Jak się do tego zabrać i czego potrzebujemy? W zasadzie musimy uzyskać informacje na temat:
– długości jednego z boków trójkąta
– wysokości trójkąta opuszczonej na ten bok
Mając te dwie informacje jesteśmy już w stanie przystąpić do obliczeń.

W naszym przypadku trójkąt ma następujące wymiary:
$a=6cm$
$h=4cm$
Pole trójkąta wynosi więc:
$$P=\frac{1}{2}\cdot6cm\cdot4cm=3cm\cdot4cm=12cm^2$$

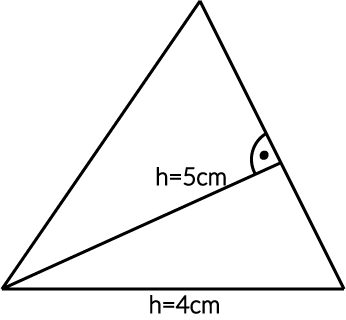
Nie wydaje się to zbyt trudne, ale jest kilka pułapek, na których dość łatwo jest zgubić punkty. Spójrz na poniższy przykład:

Przykład 2. Podstawa trójkąta jest równa $4cm$, a wysokość opuszczona na jeden z boków jest równa $5cm$. Czy to znaczy, że pole trójkąta jest równe $P=\frac{1}{2}\cdot4cm\cdot5cm=2cm\cdot5cm=10cm^2$?

Odpowiedź: NIE! Aby obliczyć pole trójkąta musimy mieć długość boku i wysokość, która jest opuszczona na tę podstawę. W naszym przypadku wysokość jest opuszczona z innego boku, niż z tego którego znamy długość, więc nie możemy jej wziąć pod uwagę dokonując obliczeń. W tym przypadku nie jesteśmy w stanie obliczyć pola trójkąta.

Przykład 3. Zostańmy jeszcze na chwilę przy trójkącie z drugiego przykładu. Gdybym Ci powiedział, że jego pole powierzchni jest równe $12cm^2$, to czy potrafiłbyś podać wysokość, jaka jest opuszczona na bok o długości $4cm$? Spójrzmy na dane, którymi dysponujemy:
$$P=12cm^2 \\
a=4cm \\
h=?$$
Zapiszmy sobie te informacje w formie wzoru matematycznego z podstawionymi danymi:
$$\frac{1}{2}\cdot4cm\cdot h=12cm^2 \\
2cm\cdot h=12cm^2$$

Z powyższych obliczeń wynika, że naszą wysokością $h$ będzie taka liczba, która po pomnożeniu przez $2$ da wynik równy $12$. Tabliczkę mnożenia znamy już do perfekcji, więc nie jest to dla nas żaden problem – szukaną liczbą jest oczywiście $6$. To znaczy, że wysokość naszego trójkąta opuszczona na podstawę o długości $4cm$ jest równa $6cm$.

To ostatnie zadanie jest dość istotne, bo pokazuje Ci, że wzór na pole dowolnej figury geometrycznej można wykorzystać nie tylko do obliczenia samego pola, ale także innych długości/wysokości, które nie zostały podane w zadaniu. Miej to zawsze na uwadze i pamiętaj, by obliczając pole zwracać uwagę na to jaka wysokość i długość boku jest podana w treści.

Pamiętaj:
Pole trójkąta jest równe połowie iloczynu długości boku i wysokości opuszczonej na ten bok.

Poniżej znajdziesz wszystkie wzory na pole trójkąta w tym te unikatowe, które bardzo często potrafią ułatwić rozwiązywanie nietypowych zadań matematycznych. Te wzory przydadzą Ci się w szczególności w gimnazjum, technikum i liceum:

Wzory na pole trójkąta:	Przykład trójkąta:
Podstawowy wzór na pole trójkąta: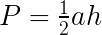 a - długość podstawy trójkąta h - długość wysokości (opuszczonej na bok a)
Wzór na pole trójkąta z sinusem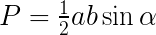 a, b - długości boków trójkąta α - kąt pomiędzy bokami a i b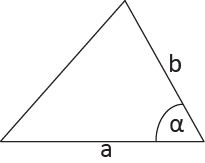
Wzór na pole trójkąta wpisanego w okrąg: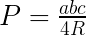 a, b, c - długości boków trójkąta R - długość promienia okręgu opisanego na trójkącie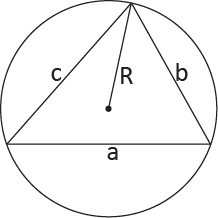
Wzór na pole trójkąta wpisanego w okrąg (podane kąty):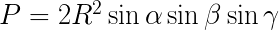 α, β, γ - kąty trójkąta R - długość promienia okręgu opisanego na trójkącie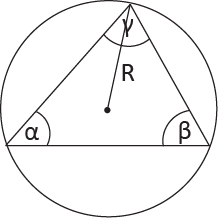
Wzór na pole trójkąta opisanego na okręgu: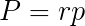 r - długość promienia okręgu wpisanego w trójkąt p - połowa sumy długości wszystkich boków trójkąta (połowa obwodu trójkąta)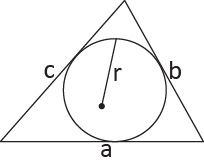
Wzór Herona: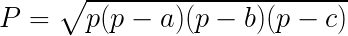 a, b, c - długości boków trójkąta p - połowa sumy długości wszystkich boków trójkąta (połowa obwodu trójkąta)