Rozwiązanie
Krok 1. Zapisanie nierówności w postaci ogólnej lub iloczynowej.
Aby przystąpić do rozwiązania tej nierówności to musimy zapisać ją w postaci iloczynowej lub ogólnej, tak aby móc obliczyć miejsca zerowe. Doprowadzenie nierówności do postaci ogólnej jest proste - wystarczy wymnożyć to co jest w nawiasie i uprościć otrzymane wyrażenia:
$$2x(1-x)+1-x\lt0 \\
2x-2x^2+1-x\lt0 \\
-2x^2+x+1\lt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Mając już postać ogólną możemy przystąpić do liczenia delty:
Współczynniki: \(a=-2,\;b=1,\;c=1\)
$$Δ=b^2-4ac=1^2-4\cdot(-2)\cdot1=1-(-8)=1+8=9 \\
\sqrt{Δ}=\sqrt{9}=3$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-1-3}{2\cdot(-2)}=\frac{-4}{-4}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-1+3}{2\cdot(-2)}=\frac{2}{-4}=-\frac{1}{2}$$
Krok 3. Szkicowanie wykresu paraboli.
Z racji tego, iż współczynnik kierunkowy \(a\) jest ujemny, to parabola będzie mieć ramiona skierowane do dołu. Zaznaczamy więc na osi wyznaczone miejsca zerowe \(x=1\) oraz \(x=-\frac{1}{2}\) (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\lt\)) i rysujemy parabolę:
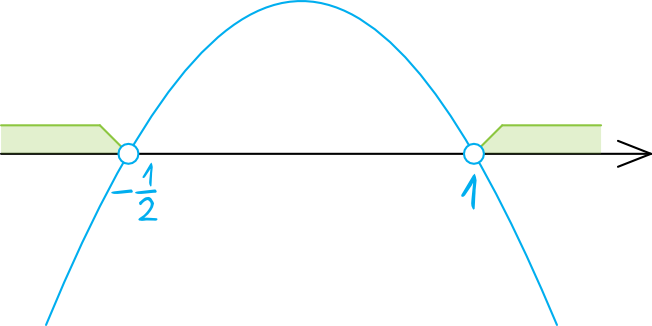
Krok 4. Odczytanie rozwiązania.
Szukamy wartości mniejszych od zera, czyli tych które znajdują się pod osią. To oznacza, że rozwiązaniem tej nierówności jest suma przedziałów:
$$x\in\left(-\infty;-\frac{1}{2}\right)\cup(1;+\infty)$$