Podstawą trójkąta równoramiennego \(ABC\) jest bok \(AB\), gdzie \(A=(2,1)\) i \(B=(5,2)\). Ramię tego trójkąta zawiera się w prostej o równaniu \(2x-y-3=0\). Oblicz współrzędne wierzchołka \(C\).
Zaznaczmy sobie poszczególne punkty w układzie współrzędnych oraz narysujmy prostą, której wzór jest podany w treści zadania i która zawiera się w jednym z ramion. Równanie naszej prostej po przekształceniu do postaci kierunkowej możemy zapisać jako \(y=2x-3\), co oznacza że współczynnik kierunkowy prostej jest dodatni. Prosta jest więc rosnąca i to właśnie na niej znajdzie się poszukiwany przez nas punkt \(C\) i jak się za chwilę okaże, znajdzie się tam też punkt \(A\).
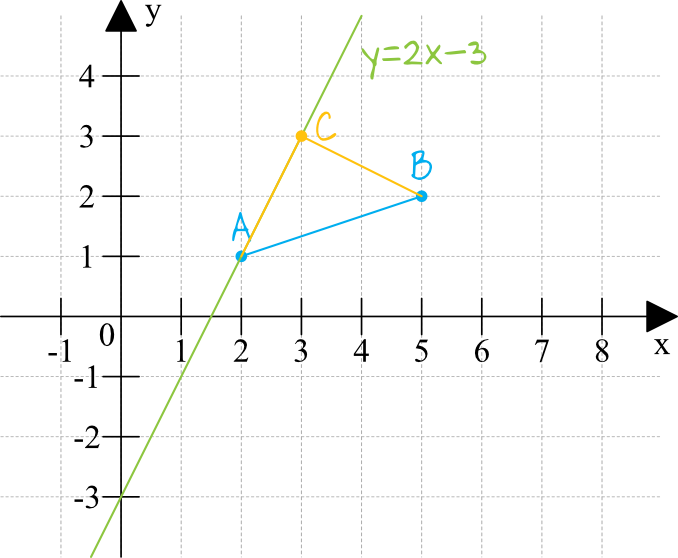
Generalnie naszym celem jest wyznaczenie współrzędnych wierzchołka \(C\). Aby go wyznaczyć musimy znać wzory dwóch prostych, z których zbudujemy układ równań, którego rozwiązaniem będą współrzędne przecięcia się prostych (czyli współrzędne punktu \(C\)). Jedną prostą już mamy (jest podana w treści zadania) i teraz musimy jakoś wyznaczyć drugą prostą, która przez ten punkt \(C\) przejdzie. Oczywiście nie wyznaczymy wzoru prostej \(BC\), no bo właśnie brakuje nam tej współrzędnej \(C\). Co wiec możemy zrobić?
Możemy wyznaczyć równanie prostej, która jest prostopadła do odcinka \(AB\) i która przechodzi przez środek tego odcinka. Ta prosta będzie na pewno przechodzić przez punkt \(C\) bo będzie to tak naprawdę wysokość trójkąta równoramiennego, a wiemy że w trójkątach równoramiennych wysokość pada dokładnie na środek podstawy. Czyli chcąc standardowo rozwiazać to zadanie moglibyśmy wyznaczyć wzór prostej \(AB\) (bo znamy odpowiednie wierzchołki), następnie wyznaczylibyśmy środek tego odcinka (wyszłoby nam, że \(S=(\frac{7}{2};\frac{3}{2})\)) no i na sam koniec wyznaczylibyśmy wzór prostej prostopadłej do prostej \(AB\), która przechodzi przez punkt \(S\). Ja jednak pokażę Ci jak można byłoby taką symetralną wyznaczyć nieco prościej:
Wiemy, że jest to trójkąt równoramienny w którym \(|AC|=|CB|\). Skoro znamy współrzędne punktów \(A\) oraz \(B\), to możemy je podstawić do wzoru na długość odcinka w układzie współrzędnych:
$$|AC|=|CB| \\
\sqrt{(x_{C}-x_{A})^2+(y_{C}-y_{A})^2}=\sqrt{(x_{B}-x_{C})^2+(y_{B}-y_{C})^2}$$
Dla przejrzystości obliczeń podnieśmy do potęgi obie strony równania i przyjmijmy że \(x_{c}=x\) oraz \(y_{c}=y\).
$$\require{cancel}
(x-x_{A})^2+(y-y_{A})^2=(x_{B}-x)^2+(y_{B}-y)^2 \\
(x-2)^2+(y-1)^2=(5-x)^2+(2-y)^2 \\
\cancel{x^2}-4x+\cancel{4}+\cancel{y^2}-2y+1=25-10x+\cancel{x^2}+\cancel{4}-4y+\cancel{y^2} \\
2y=-6x+24 \quad\bigg/:2 \\
y=-3x+12$$
Udało nam się otrzymać kolejny wzór prostej, która przechodzi przed punkt \(C\) i jest to właśnie symetralna odcinka \(AB\).
Z wyznaczonego w drugim kroku równania prostej i z równania podanego w treści zadania (który po przekształceniu jest równy \(y=2x-3\)) możemy stworzyć taki mały układ równań. Obrazowo rzecz ujmując – te dwie proste przetną się w punkcie \(C\), a wiemy z interpretacji geometrycznej układu równań, że miejsce przecięcia się dwóch prostych jest właśnie rozwiązaniem układu równań. Zatem:
\begin{cases}
y=-3x+12 \\
y=2x-3
\end{cases}
Rozwiązując metodę podstawiania otrzymamy:
$$-3x+12=2x-3 \\
15=5x \\
x=3$$
Znając współrzędną \(x\) możemy już bez problemu obliczyć współrzędną \(y\):
$$y=2x-3 \\
y=2\cdot3-3 \\
y=3$$
To oznacza, że poszukiwane przez nas współrzędne to \(C=(3;3)\).
\(C=(3;3)\)

