Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy nanieść na układ współrzędnych punkty \(A\) oraz \(C\). Korzystając dodatkowo z informacji, że będziemy mieli tutaj prostokąt, którego boki są równoległe do osi układu współrzędnych, otrzymamy taką oto sytuację:
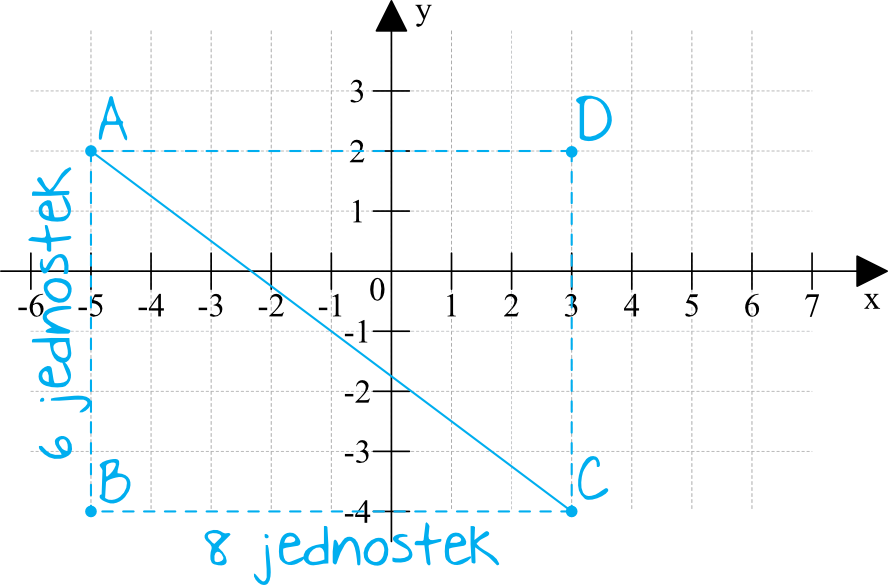
Z rysunku musimy też odczytać od razu wymiary naszego prostokąta (licząc po kratkach). Widzimy, że dolny bok ma długość \(8\) jednostek, natomiast drugi ma długość \(6\) jednostek.
Krok 2. Obliczenie długości przekątnej prostokąta.
Dwa boki prostokąta tworzą wraz z poszukiwaną przekątną trójkąt prostokątny. Korzystając z Twierdzenia Pitagorasa możemy zatem zapisać, że:
$$8^2+6^2=d^2 \\
64+36=d^2 \\
d^2=100 \\
d=10 \quad\lor\quad d=-10$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(d=10\).
Krok 3. Podanie współrzędnych pozostałych dwóch wierzchołków prostokąta.
Z rysunku wynika wprost, że punkt \(B\) musi mieć współrzędną \(x\) taką jak \(x_{A}\) i współrzędną \(y\) taką samą jak \(y_{C}\). Analogicznie punkt \(D\) musi mieć \(x\) taką jak \(x_{C}\) i współrzędną \(y\) taką samą jak \(y_{A}\). To oznacza, że brakującymi współrzędnymi wierzchołków prostokąta będą: \(B=(-5;-4)\) oraz \(D=(3;2)\).
Oczywiście równie dobrą odpowiedzią byłoby \(B=(3;2)\) oraz \(D=(-5;-4)\) (w zależności od tego jak podpisaliśmy wierzchołki prostokąta).