Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczmy w układzie współrzędnych dwa wskazane wierzchołki i zobaczmy co z tego możemy otrzymać:
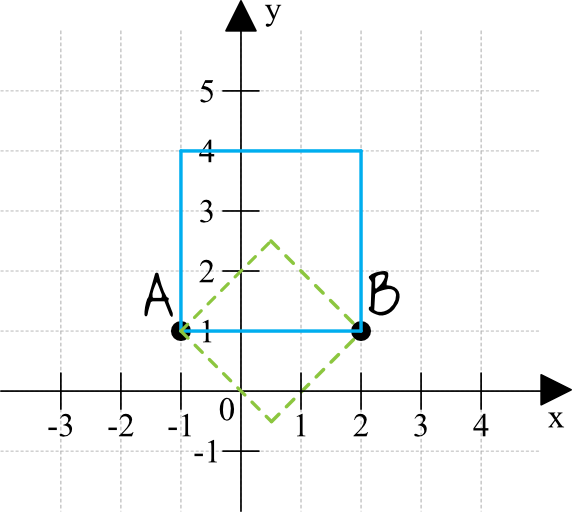
Tu powinniśmy dostrzec, że zaznaczony odcinek może być bokiem kwadratu, ale może też być jego przekątną, co sprawi że otrzymamy w tym zadaniu tak naprawdę dwie różne odpowiedzi.
Krok 2. Obliczenie długości odcinka \(AB\).
Z rysunku jasno wynika, że odcinek \(AB\) ma długość \(3\). Gdybyśmy jednak nie dostrzegli tego (albo gdyby nie było to takie oczywiste do odczytania) to możemy posłużyć się wzorem na długość odcinka w układzie współrzędnych:
$$|AB|=\sqrt{(x_{B}-x_{A})^2+(y_{B}-y_{A})^2} \\
|AB|=\sqrt{(2-(-1))^2+(1-1)^2} \\
|AB|=\sqrt{3^2+0^2} \\
|AB|=\sqrt{9} \\
|AB|=3$$
Krok 3. Obliczenie pola kwadratu.
I tu właśnie rozpatrujemy dwie możliwości:
• Pierwsza możliwość - jeżeli odcinek \(AB\) jest bokiem kwadratu, to:
$$P=a^2 \\
P=3^2 \\
P=9$$
• Druga możliwość - jeżeli odcinek \(AB\) jest przekątną kwadratu, to wiedząc że przekątna kwadratu o boku \(a\) ma długość \(a\sqrt{2}\) możemy zapisać, że:
$$a\sqrt{2}=3 \\
a=\frac{3}{\sqrt{2}}$$
Moglibyśmy usunąć jeszcze niewymierność z mianownika, otrzymalibyśmy wtedy \(\frac{3\sqrt{2}}{2}\), ale tak prawdę mówiąc, to nie trzeba wykonywać tej operacji, bo obliczając pole powierzchni i tak pozbędziemy się pierwiastka. Skoro więc \(a=\frac{3}{\sqrt{2}}\), to pole powierzchni będzie równe:
$$P=a^2 \\
P=\left(\frac{3}{\sqrt{2}}\right)^2 \\
P=\frac{9}{2}=4,5$$