Objętość ostrosłupa prawidłowego trójkątnego ABCS jest równa 27√3. Długość krawędzi AB podstawy ostrosłupa

Objętość ostrosłupa prawidłowego trójkątnego $ABCS$ jest równa $27\sqrt{3}$. Długość krawędzi $AB$ podstawy ostrosłupa jest równa $6$ (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.

Rozwiązanie:

Krok 1. Obliczenie pola powierzchni podstawy ostrosłupa.

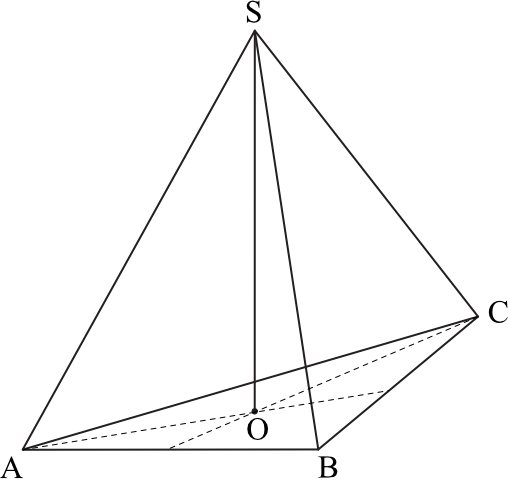
Musimy sobie ustalić jaka to figura znajduje się w podstawie naszej bryły. Skoro jest to ostrosłup prawidłowy trójkątny, to w podstawie znajduje się trójkąt równoboczny. Podaną mamy też długość boku tego trójkąta i jest ona równa $6$. Policzenie pola podstawy jest więc bardzo proste, bo skoro jest to trójkąt równoboczny to skorzystamy z następującego wzoru:
$$P_{p}=\frac{a^2\sqrt{3}}{4} \\
P_{p}=\frac{6^2\sqrt{3}}{4} \\
P_{p}=9\sqrt{3}$$

Krok 2. Obliczenie wysokości ostrosłupa.

Znamy pole powierzchni podstawy, znamy też objętość naszej bryły, więc policzymy wysokość ostrosłupa. Przyda nam się ona w późniejszych krokach do wyznaczenia długości ściany bocznej.
$$V=\frac{1}{3}P_{p}\cdot H \\
27\sqrt{3}=\frac{1}{3}\cdot9\sqrt{3}\cdot H \\
27\sqrt{3}=3\sqrt{3}\cdot H \\
H=9$$

Krok 3. Obliczenie długości odcinka $AD$ oraz $|OD|$.

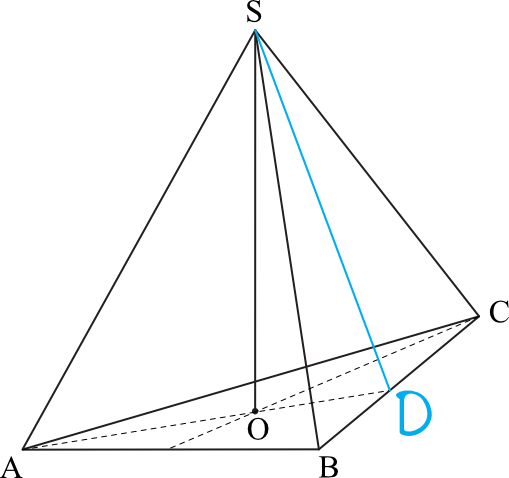
Spójrzmy teraz na rysunek i na trójkąt $ODS$. Długość odcinka $SO$ obliczyliśmy przed chwilą. Musimy jeszcze obliczyć długość odcinka $OD$ i wtedy z Twierdzenia Pitagorasa wyznaczymy wysokość ściany bocznej.

Z własności trójkąta równobocznego wiemy, że odcinek $OD$ jest równy $\frac{1}{3}$ długości wysokości trójkąta.
Wysokość trójkąta, czyli bok $|AD|$ jest równy:
$$|AD|=\frac{a\sqrt{3}}{2} \\
|AD|=\frac{6\sqrt{3}}{2} \\
|AD|=3\sqrt{3}$$

Tak więc $|OD|=\frac{1}{3}\cdot3\sqrt{3}=\sqrt{3}$.

Krok 4. Obliczenie wysokości ściany bocznej.

Teraz bez przeszkód możemy obliczyć wysokość trójkąta w ścianie bocznej:
$$a^2+b^2=c^2 \\
|SO|^2+|OD|^2=|SD|^2 \\
9^2+(\sqrt{3})^2=|SD|^2 \\
81+3=|SD|^2 \\
|SD|=\sqrt{84}=\sqrt{4\cdot21}=2\sqrt{21}$$

Krok 5. Obliczenie pola powierzchni ściany bocznej.

Obliczmy teraz pole pojedynczej ściany bocznej naszego ostrosłupa:
$$P_{b}=\frac{1}{2}a\cdot h \\
P_{b}=\frac{1}{2}\cdot6\cdot2\sqrt{21} \\
P_{b}=6\sqrt{21}$$

Krok 6. Obliczenie pola całkowitego ostrosłupa.

$$P_{c}=P_{p}+3\cdot P_{b} \\
P_{c}=9\sqrt{3}+3\cdot6\sqrt{21} \\
P_{c}=9\sqrt{3}+18\sqrt{21}$$

Otrzymana postać jest chyba najlepszą możliwą do otrzymania. Alternatywnie moglibyśmy zapisać to jako $P_{c}=9\sqrt{3}\cdot(1+2\sqrt{7})$ lub też obliczyć przybliżenie tej liczby jako $\approx98,07$.

Odpowiedź:

$P_{c}=9\sqrt{3}\cdot(1+2\sqrt{7})$

Zadania

Objętość ostrosłupa prawidłowego trójkątnego ABCS jest równa 27√3. Długość krawędzi AB podstawy ostrosłupa

Objętość ostrosłupa prawidłowego trójkątnego \(ABCS\) jest równa \(27\sqrt{3}\). Długość krawędzi \(AB\) podstawy ostrosłupa jest równa \(6\) (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.