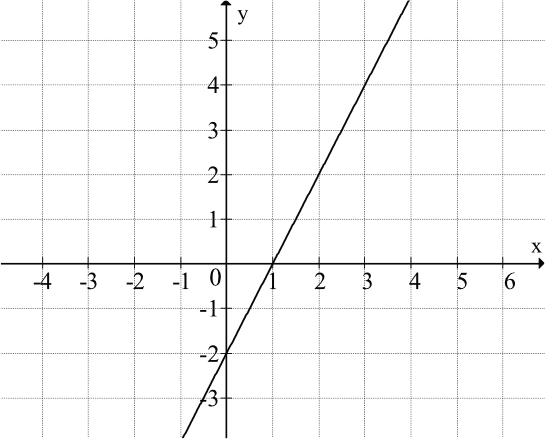
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej \(f\), przy czym \(f(0)=-2\) i \(f(1)=0\).
Wykres funkcji \(g\) jest symetryczny do wykresu funkcji \(f\) względem początku układu współrzędnych. Funkcja \(g\) jest określona wzorem:
Nie jest to krok obowiązkowy, ale z pewnością ułatwi nam wybór prawidłowej odpowiedzi. To co najważniejsze w tym rysunku to fakt, że dzięki niemu widzimy wyraźnie, że funkcja \(g(x)\) przecina oś \(Oy\) w miejscu \(A=(0;2)\). Przyda nam się to do wyznaczenia współczynnika \(b\).
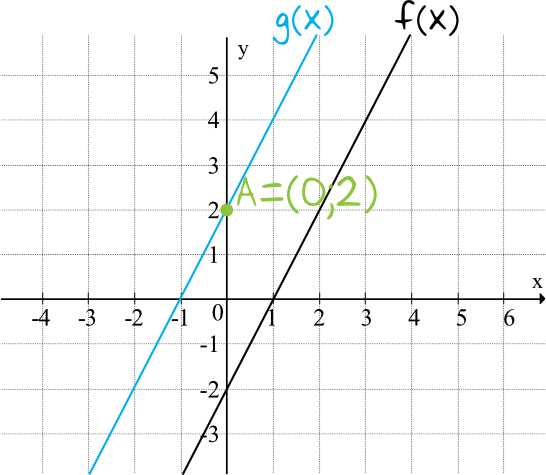
Funkcja \(g(x)\) jest funkcją liniową, tak więc możemy zapisać ją w postaci \(g(x)=ax+b\). Aby poznać pełny wzór funkcji musimy obliczyć (albo odczytać z wykresu) wartości współczynników \(a\) oraz \(b\). Zacznijmy od współczynnika \(b\), który bardzo szybko odczytamy z miejsca przecięcia się wykresu funkcji z osią \(Oy\). Skoro prosta przecina oś \(Oy\) na wysokości dwóch jednostek, to \(b=2\).
W ten oto sposób wiemy już, że prawidłowa jest albo pierwsza, albo trzecia odpowiedź.
Funkcja \(g(x)\) jest funkcją rosnącą. To oznacza, że współczynnik \(a\) musi być dodatni, więc pasowałyby nam tylko dwie pierwsze odpowiedzi. Drugą odpowiedź odrzuciliśmy jednak już wcześniej ze względu na współczynnik \(b=2\). W ten oto sposób wiemy już, że nasza funkcja ma następujący wzór: \(g(x)=2x+2\).
A. \(g(x)=2x+2\)

