Pole powierzchni całkowitej stożka możemy obliczyć korzystając z następującego wzoru:
$$P_{c}=πr^2+πrl$$
gdzie:
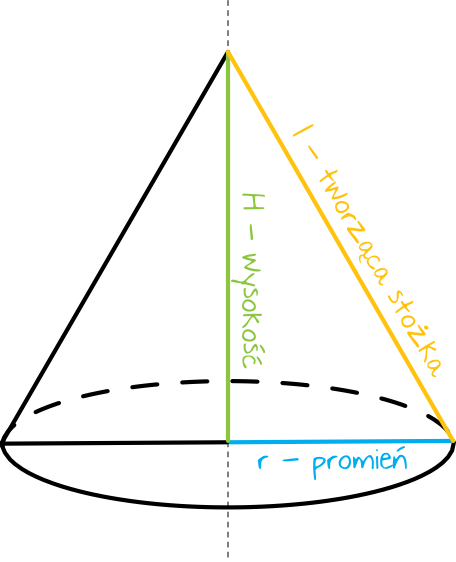
\(P_{c}\) – pole powierzchni całkowitej stożka
\(r\) – promień podstawy stożka
\(l\) – tworząca stożka
W różnych tablicach i podręcznikach możemy się też jeszcze spotkać z lekko przekształconą postacią tego wzoru:
$$P_{c}=πr(r+l)$$
To o czym musimy sobie jeszcze powiedzieć w tym temacie to pole powierzchni bocznej stożka.
Pole powierzchni bocznej obliczymy korzystając ze wzoru:
$$P_{b}=πrl$$
gdzie:
\(P_{b}\) – pole powierzchni bocznej stożka
\(r\) – promień podstawy stożka
\(l\) – tworząca stożka
Teraz jak się dobrze przyjrzymy tym wzorom to zauważymy, że pole powierzchni całkowitej stożka to tak naprawdę suma pola podstawy (która jest kołem) oraz pola powierzchni bocznej. Moglibyśmy więc zapisać, że \(P_{c}=P_{p}+P_{b}\).
Zobaczmy zatem jak wykorzystujemy w praktyce te wszystkie poznane wzory.
Podstawiając znane nam dane do wzoru na pole powierzchni całkowitej stożka otrzymamy:
$$P_{c}=πr^2+πrl \\
P_{c}=π\cdot5^2+π \cdot5\cdot8 \quad\bigg/:π \\
P_{c}=25π+40π \\
P_{c}=65π$$
Krok 1. Obliczenie długości promienia podstawy.
Korzystając z wiedzy na temat pola powierzchni bocznej oraz długości tworzącej stożka możemy obliczyć brakującą długość promienia podstawy:
$$P_{b}=πrl \\
20π=πr\cdot5 \\
5r=20 \\
r=4$$
Krok 2. Obliczenie pola powierzchni całkowitej.
Znamy już wszystkie potrzebne miary zatem możemy zapisać, że:
$$P_{c}=πr^2+πrl \\
P_{c}=π\cdot4^2+π\cdot4\cdot5 \\
P_{c}=16π+20π \\
P_{c}=36π$$
Oczywiście mogliśmy od razu podstawić pod \(πrl\) wartość \(20π\), bo to jest przecież nasze pole powierzchni bocznej.
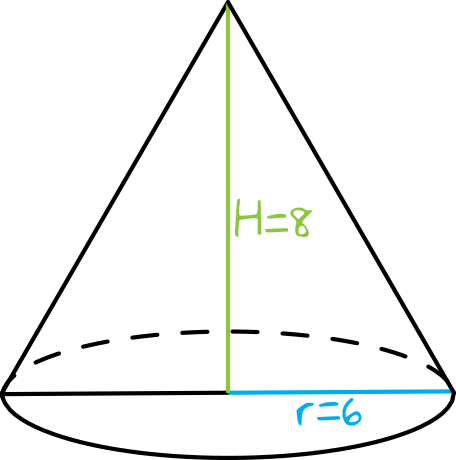
Krok 1. Obliczenie długości tworzącej stożka.
Spójrzmy na trójkąt prostokątny, który tworzą promień podstawy, wysokość stożka oraz tworząca stożka. Znamy dwie miary w tym trójkącie, zatem brakującą tworzącą stożka możemy obliczyć korzystając z Twierdzenia Pitagorasa:
$$6^2+8^2=l^2 \\
36+64=l^2 \\
l^2=100 \\
l=10 \quad\lor\quad l=-10$$
Tworząca stożka nie może być ujemna, bo długości boków zawsze są dodatnie, zatem zostaje nam \(l=10\).
Krok 2. Obliczenie pola powierzchni całkowitej.
Korzystając ze wzoru na pole powierzchni całkowitej możemy zapisać, że:
$$P_{c}=πr^2+πrl \\
P_{c}=π\cdot6^2+π\cdot6\cdot10 \\
P_{c}=36π+60π \\
P_{c}=96π$$
