Rozwiązanie
Krok 1. Zapisanie współrzędnych wierzchołka paraboli.
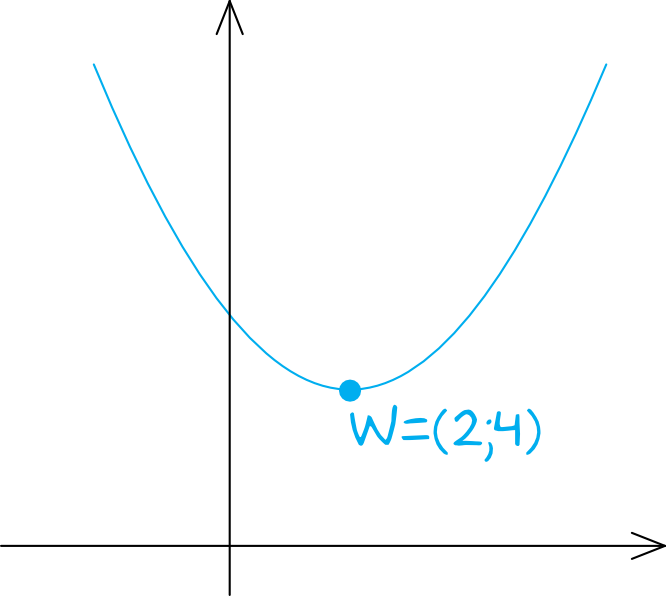
Z treści zadania wynika, że nasza funkcja kwadratowa ma ramiona skierowane do góry (przed \(x^2\) nie stoi żadna liczba, więc współczynnik \(a=1\)) i że przyjmuje ona najmniejszą wartość \(y=4\) dla argumentu \(x=2\). W przypadku tej funkcji kwadratowej ta najmniejsza wartość musi być przyjmowana w wierzchołku \(W=(p;q)\), a to oznacza, że \(W=(2;4)\).
Krok 2. Obliczenie wartości współczynnika \(b\).
Skorzystamy ze wzoru na pierwszą współrzędną wierzchołka paraboli, czyli \(p=\frac{-b}{2a}\). Podstawiając do tego wzoru \(p=2\) oraz \(a=1\), otrzymamy:
$$2=\frac{-b}{2\cdot1} \\
2=\frac{-b}{2} \\
4=-b \\
b=-4$$
Krok 3. Obliczenie wartości współczynnika \(c\).
Znając wartość współczynnika \(b\), możemy wrócić do wzoru naszej funkcji i podstawić do niej wszystkie znane nam dane, otrzymując:
$$4=2^2-4\cdot2+c \\
4=4-8+c \\
4=-4+c \\
c=8$$