Funkcja kwadratowa \(f\) określona jest wzorem \(f(x)=ax^2+bx+c\). Zbiorem rozwiązań nierówności \(f(x)\gt0\) jest przedział \((0,12)\). Największa wartość funkcji \(f\) jest równa \(9\). Oblicz współczynniki \(a\), \(b\) i \(c\) funkcji \(f\).
Musimy się zastanowić jak będzie wyglądać nasza parabola.
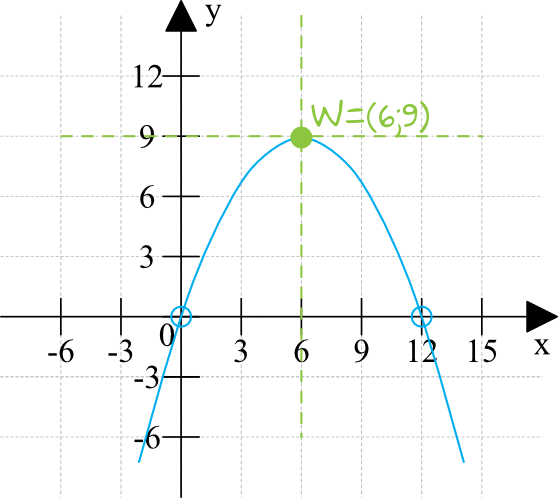
Wniosek I – Skoro funkcja przyjmuje wartości dodatnie (\(f(x)\gt0\)) tylko w przedziale \((0;12)\), to musi być to parabola z ramionami skierowanymi do dołu (patrz rysunek). Nie ma innej możliwości.
Wniosek II – Czym jest natomiast przedział \((0;12)\)? Kiedy rozwiązujemy standardową nierówność i podajemy jej rozwiązania, to zawsze na krańcach przedziałów znajdują się tak naprawdę miejsca zerowe (które obliczamy np. z delty albo z postaci iloczynowej). Nie inaczej jest tutaj, zatem z tego przedziału możemy odczytać, że funkcja ta przecina oś \(Ox\) w punktach \(x_{1}=0\) oraz \(x_{2}=12\) (patrz rysunek).
Wniosek III – Jakie współrzędne ma wierzchołek paraboli? Skoro największa wartość funkcji jest równa \(9\), to jedną współrzędną (\(y=9\)) już znamy. Wiemy też, że wierzchołek paraboli znajduje się dokładnie po środku, między miejscami zerowymi. Zatem współrzędne wierzchołka to \(W=(6;9)\).
Dzięki trzeciemu wnioskowi z pierwszego kroku jesteśmy w stanie zapisać równanie tej paraboli w postaci kanonicznej. Funkcję o wierzchołku w punkcie \(W=(p;q)\) możemy opisać wzorem:
$$y=a(x-p)^2+q \\
y=a(x-6)^2+9$$
Wiemy, że parabola przechodzi między innymi przez punkt \((0;0)\), zatem możemy podstawić współrzędne tego punktu do wyznaczonego przed chwilą wzoru i tym samym obliczyć wartość współczynnika \(a\):
$$0=a\cdot(0-6)^2+9 \\
0=a\cdot(-6)^2+9 \\
0=36a+9 \\
36a=-9 \\
a=-\frac{9}{36}=-\frac{1}{4}$$
Podstawiając wyznaczony współczynnik \(a=-\frac{1}{4}\) do wzoru z kroku drugiego, będziemy tak naprawdę znać już pełny wzór naszej funkcji:
$$y=-\frac{1}{4}(x-6)^2+9$$
To jednak nie koniec, bo zgodnie z treścią zadania musimy przedstawić wzór tej funkcji w postaci ogólnej typu \(f(x)=ax^2+bx+c\) i wypisać poszczególne współczynniki. Zatem:
$$y=-\frac{1}{4}(x-6)^2+9 \\
y=-\frac{1}{4}(x^2-12x+36)+9 \\
y=-\frac{1}{4}x^2+3x-9+9 \\
y=-\frac{1}{4}x^2+3x$$
Poszukiwanymi współczynnikami są więc: \(a=-\frac{1}{4}, b=3, c=0\).
\(a=-\frac{1}{4}, b=3, c=0\)


Dzięki
Bardzo dobrze wytłumaczone
„a” nie powinno być ujemne skoro parabola idzie w dół? Ma to wpływ na wynik, powinno być a = – ¼
Ale przecież w 3. kroku właśnie wyszło, że a=-1/4 ;)
Czy mógłbyś wytłumaczyć czemu musi być skierowana w dół?
Ah, to chyba dlatego, że skoro tylko w tym przedziale to musi być do dołu bo wtedy na dole jest (-nieskończoność,0)U(12,+nieskończoność) tak?
Dość dobrze opisałem to w pierwszym wniosku – gdyby funkcja miała ramiona skierowane do góry, to wartości dodatnie byłyby przyjmowane np. w plus nieskończoności, a tutaj muszą być przyjmowane w konkretnym przedziale od 0 do 12 :) Poza tym o tym, że parabola ma ramiona skierowane w dół świadczy jeszcze fakt, że przyjmuje ona największą wartość równą 9. Gdyby ramiona paraboli były skierowane do góry, to największą wartością byłoby zawsze plus nieskończoność :)