W trójkącie równoramiennym \(ABC\) spełnione są warunki: \(|AC|=|BC|\), \(|\sphericalangle CAB|=50°\). Odcinek \(BD\) jest dwusieczną kąta \(ABC\), a odcinek \(BE\) jest wysokością opuszczoną z wierzchołka \(B\) na bok \(AC\). Miara kąta \(EBD\) jest równa:
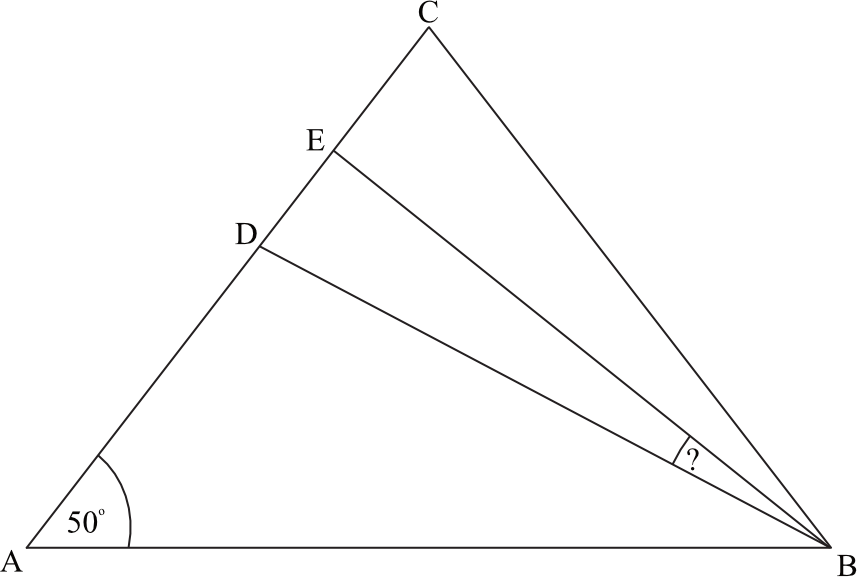
Z treści wynika że podstawą jest bok \(AB\), bo równej długości są odcinki \(|AC|=|BC|\). Kąty przy podstawie trójkąta równoramiennego mają jednakową miarę, zatem skoro \(|\sphericalangle CAB|=50°\), to możemy zapisać, że:
$$|\sphericalangle CAB|=|\sphericalangle ABC|=50°$$
Skoro odcinek \(BD\) jest dwusieczną kąta \(ABC\), to miara kąta \(ABD\) jest równa:
$$|\sphericalangle ABD|=50°:2=25°$$
Analogicznie: |\sphericalangle DBC|=50°:2=25°
Wbrew pozorom odcinek \(BE\) wcale nie jest dwusieczną kąta \(DBC\), co prowadziłoby nas do błędnej odpowiedzi \(12,5°\). Miarę poszukiwanego kąta musimy wyznaczyć korzystając z trójkąta \(ABE\). Jest to na pewno trójkąt prostokątny, bo odcinek \(EB\) jest wysokością trójkąta, a wysokość zawsze pada pod kątem prostym. W ten sposób obliczymy miarę kąta \(ABE\), co z kolei pozwoli nam wyznaczyć wartość kąta \(EBD\). Zatem:
$$|\sphericalangle ABE|=180°-90°-50°=40°$$
Miara kąta \(EBD\) jest różnicą między kątem \(ABE\) oraz \(ABD\):
$$|\sphericalangle EBD|=|\sphericalangle ABE|-|\sphericalangle ABD|=40°-25°=15°$$
D. \(15°\)

