Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Z treści zadania wynika, że stosunek wysokości tych stożków jest równy \(3:2\), czyli możemy zapisać, że mały stożek ma wysokość równą \(2x\), natomiast duży stożek ma wysokość \(3x\).
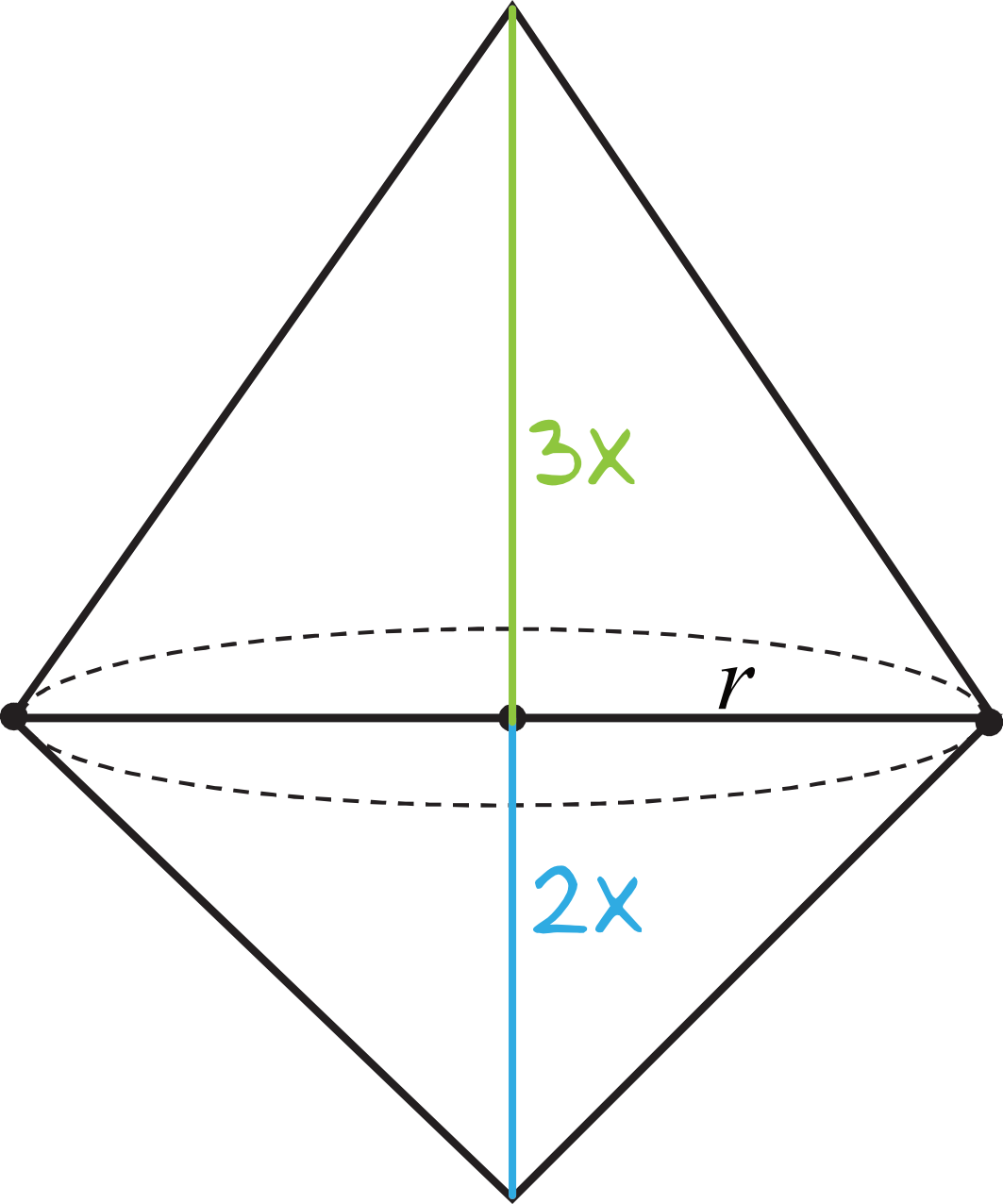
Możemy nawet obrazowo powiedzieć, że wysokość dużego stożka jest \(1,5\) raza większa od wysokości małego stożka.
Krok 2. Obliczenie objętości dużego stożka.
Objętość stożka obliczylibyśmy ze wzoru:
$$V=\frac{1}{3}P_{p}\cdot H$$
Jeden i drugi stożek mają to same pole podstawy. To co je różni to jedynie wysokość. Skoro wysokość dużego stożka jest \(1,5\) raza większa od wysokości małego stożka, a obie bryły mają jednakową podstawę, to objętość dużego stożka musi być \(1,5\) raza większa od objętości małego stożka. W związku z tym:
$$V_{d}=1,5\cdot12cm^3 \\
V_{d}=18cm^3$$
Krok 3. Obliczenie sumy objętości małego i dużego stożka.
Na koniec musimy zsumować objętości małego i dużego stożka:
$$V=12cm^3+18cm^3=30cm^3$$