Rozwiązanie
Krok 1. Obliczenie pola powierzchni pierwszego dachu.
Zacznijmy od obliczenia pola powierzchni pierwszego dachu. Dach składa się z czterech trójkątów równobocznych o boku długości \(8cm\). Musimy więc wyznaczyć pole każdego takiego trójkąta i pomnożyć to przez \(4\). Wyznaczyć pole tego trójkąta można tak naprawdę na dwa sposoby:
I sposób - korzystając ze wzoru na pole trójkąta równobocznego.
Wzór na pole trójkąta równobocznego jest następujący:
$$P=\frac{a^2\sqrt{3}}{4} \\
P=\frac{8^2\sqrt{3}}{4} \\
P=\frac{64\sqrt{3}}{4} \\
P=16\sqrt{3}$$
Skoro mamy cztery takie trójkąty, to pole powierzchni dachu będzie równe:
$$P_{1}=4\cdot16\sqrt{3}=64\sqrt{3}$$
II sposób - wyznaczając wysokość trójkąta równobocznego.
Tym razem możemy skorzystać ze wzoru na wysokość trójkąta równobocznego:
$$h=\frac{a\sqrt{3}}{2} \\
h=\frac{8\sqrt{3}}{2} \\
h=4\sqrt{3}$$
Jeśli tego wzoru nie pamiętamy, to ostatecznie możemy wyznaczyć wysokość z Twierdzenia Pitagorasa, wiedząc że wysokość trójkąta równobocznego dzieli podstawę na dwie równe części:
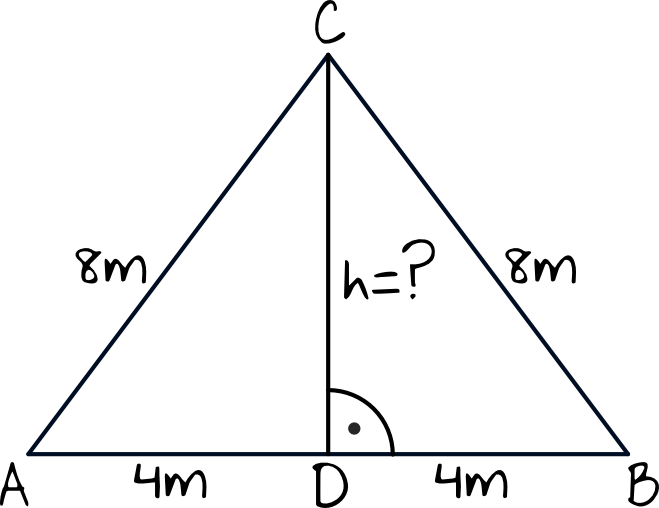
$$4^2+h^2=8^2 \\
16+h^2=64 \\
h^2=48 \\
h=\sqrt{48}=4\sqrt{3}$$
Znając wysokość trójkąta równobocznego możemy obliczyć już bez przeszkód jego pole standardowym wzorem na pole trójkąta:
$$P=\frac{1}{2}ah \\
P=\frac{1}{2}\cdot8\cdot4\sqrt{3} \\
P=4\cdot4\sqrt{3} \\
P=16\sqrt{3}$$
Skoro mamy cztery takie trójkąty, to pole powierzchni dachu będzie równe:
$$P_{1}=4\cdot16\sqrt{3}=64\sqrt{3}$$
Krok 2. Obliczenie pola powierzchni drugiego dachu.
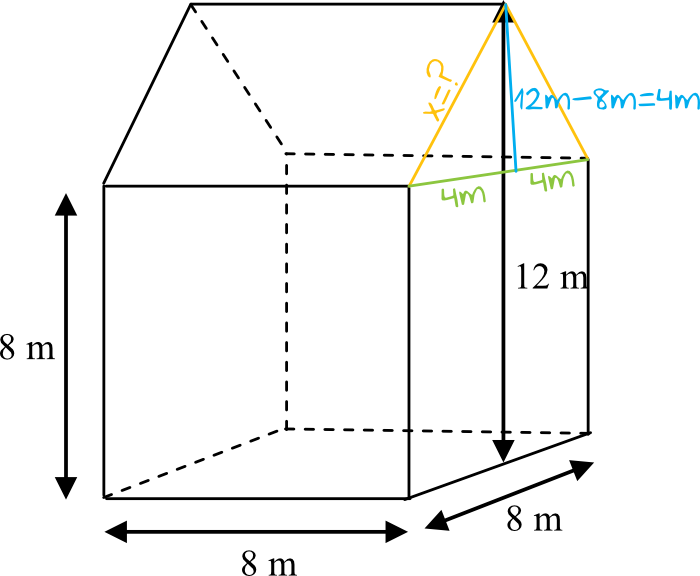
Do obliczenia pola powierzchni drugiego dachu (składającego się z dwóch prostokątów) potrzebujemy znać długość krótszego boku prostokąta. Obliczymy go z Twierdzenia Pitagorasa i trójkąta zaznaczonego na powyższym rysunku:
$$4^2+4^2=x^2 \\
16+16=x^2 \\
x^2=32 \\
x=\sqrt{32}=4\sqrt{2}$$
W związku z tym pojedynczy kawałek dachu jest prostokątem o wymiarach \(8\times4\sqrt{2}\), zatem jego pole powierzchni będzie równe:
$$P=8\cdot4\sqrt{2} \\
P=32\sqrt{2}$$
Nasz drugi dach składa się z dwóch takich prostokątów, zatem jego pole powierzchni będzie równe:
$$P_{2}=2\cdot32\sqrt{2} \\
P_{2}=64\sqrt{2}$$
Krok 3. Określenie który dach ma większą powierzchnię.
Pierwszy dach ma powierzchnię \(64\sqrt{3}\), drugi dach ma powierzchnię \(64\sqrt{2}\), zatem to pierwszy dach ma tę powierzchnię większą:
$$64\sqrt{3}\gt64\sqrt{2} \\
P_{1}\gt P_{2}$$