Rozwiązanie
Krok 1. Zapisanie równań.
Z treści zadania wynika, że liny użyjemy na długości dwóch boków \(a\) oraz jednego boku \(b\), więc możemy zapisać, że:
$$2a+b=200$$
Dodatkowo wiemy, że pole powierzchni kąpieliska w kształcie prostokąta obliczymy ze wzoru:
$$P=a\cdot b$$
Krok 2. Zapisanie wzoru funkcji \(P(x)\).
Kluczem do sukcesu będzie zapisanie pola powierzchni w postaci funkcji z jedną zmienną, czyli zmienną \(a\). Chcąc tego dokonać, wyznaczmy wartość \(b\) z równania \(2a+b=200\), czyli:
$$2a+b=200 \\
b=200-2a$$
Podstawiając teraz \(b=200-2a\) do równania \(P=a\cdot b\), otrzymamy:
$$P=a\cdot(200-2a) \\
P=200a-2a^2 \\
P=-2a^2+200a$$
Otrzymaliśmy informację, że pole powierzchni kąpieliska można opisać wzorem \(-2a^2+200a\). I teraz następuje kluczowy moment w tego typu zadaniach - musimy całość potraktować jak funkcję kwadratową (dla jakiejś wartości \(a\) otrzymamy konkretną wartość \(P\)). Zapisalibyśmy więc, że \(P(a)=-2a^2+200a\).
Krok 3. Wyznaczenie współrzędnych wierzchołka paraboli.
Wykresem funkcji kwadratowej jest parabola. Nasza parabola będzie mieć ramiona skierowane do dołu (bo współczynnik \(a=-2\)). To sprawia, że nasza funkcja będzie wyglądać mniej więcej w ten oto sposób:
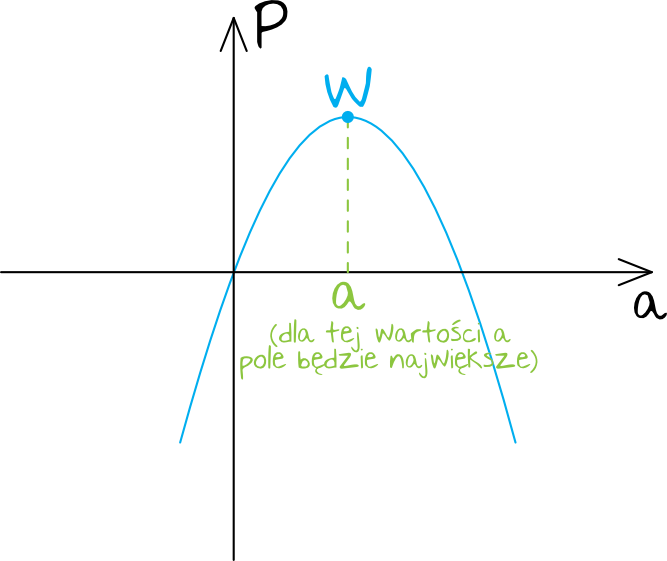
Celem zadania jest dowiedzenie się, dla jakiego \(a\) pole powierzchni \(P\) będzie największe. Z własności funkcji kwadratowych wiemy, że ta największa wartość będzie osiągnięta w wierzchołku. Musimy zatem obliczyć dla jakiej długości \(a\) ta największa wartość jest przyjmowana. W tym celu skorzystamy ze wzoru na współrzędną \(x_{W}\) wierzchołka paraboli:
$$x_{W}=\frac{-b}{2a}$$
Do tego wzoru podstawiamy współczynniki \(a\) oraz \(b\) naszej funkcji kwadratowej (nie mylmy tego z bokami \(a\) oraz \(b\), to jedynie zbieżność symboli). W przypadku funkcji \(P(a)=-2a^2+200a\) widzimy, że współczynnik \(a=-2\) oraz \(b=200\), zatem:
$$x_{W}=\frac{-200}{2\cdot(-2)} \\
x_{W}=\frac{-200}{-4} \\
x_{W}=50$$
To oznacza, że największe pole powierzchni osiągniemy, gdy długość boku \(a\) będzie równa \(50\).
Krok 4. Obliczenie długości boku \(b\)
Celem zadania jest podanie wszystkich wymiarów naszego kąpieliska, zatem obliczmy jeszcze długość boku \(b\). W tym celu wystarczy do równania \(b=200-2a\) podstawić obliczone przed chwilą \(a=50\), zatem:
$$b=200-2\cdot50 \\
b=200-100 \\
b=100$$
To oznacza, że kąpielisko będzie mieć największe pole gdy \(a=50\) oraz \(b=100\).