Dany jest stożek, którego przekrojem osiowym jest trójkąt o bokach długości: 6, 10 i 10

Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc na rysunek dane z treści zadania otrzymamy następującą sytuację:



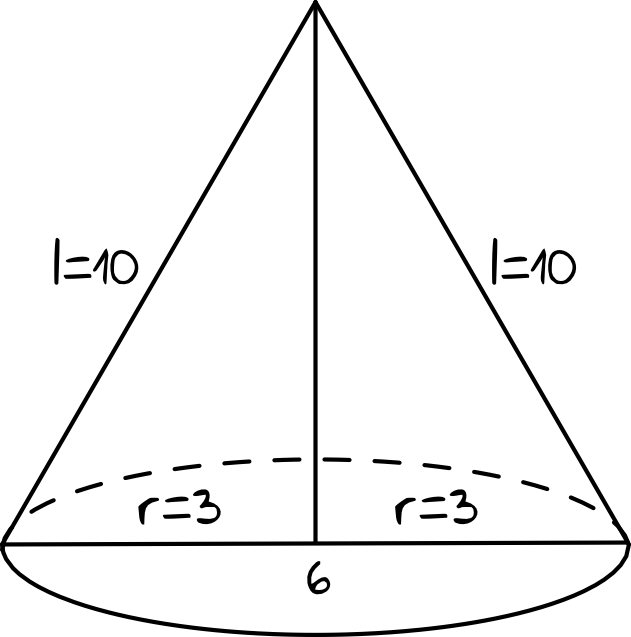
Krok 2. Obliczenie stosunku pola powierzchni bocznej do pola podstawy.
Musimy obliczyć stosunek pola powierzchni bocznej do pola podstawy czyli:
$$\require{cancel}\frac{P_{b}}{P_{p}}=\frac{πrl}{πr^2} \\
\frac{P_{b}}{P_{p}}=\frac{\cancel{π}\cdot\cancel{r}\cdot l}{\cancel{π}\cdot\cancel{r}\cdot r} \\
\frac{P_{b}}{P_{p}}=\frac{l}{r} \\
\frac{P_{b}}{P_{p}}=\frac{10}{3}$$