Rozwiązanie
Krok 1. Zapisanie nierówności w postaci ogólnej.
Aby przystąpić do wykonywania obliczeń musimy zapisać tę nierówność w postaci ogólnej. Musimy zatem wykonać potęgowanie i przenieść wszystkie wyrazy na lewą stronę, pozostawiając po prawej stronie samo zero.
Uwaga: Jeżeli przeniesiemy \((2-5x)^2\) na lewą stronę to nie powstanie nam wbrew pozorom postać iloczynowa, z której to potem łatwo wyznaczymy miejsca zerowe. Po przeniesieniu po lewej stronie powstanie nam \((4x-1)^2-(2-5x)^2\). Gdyby zamiast minusa między nawiasami było mnożenie, to wtedy byłaby to postać iloczynowa, a tak to niestety musimy wykonywać potęgowanie i potem liczyć całość z delty.
$$(4x-1)^2\lt(2-5x)^2 \\
16x^2-8x+1\lt4-20x+25x^2 \\
-9x^2+12x-3\lt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=-9,\;b=12,\;c=-3\)
$$Δ=b^2-4ac=12^2-4\cdot(-9)\cdot(-3)=144-108=36 \\
\sqrt{Δ}=\sqrt{36}=6$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-12-6}{2\cdot(-9)}=\frac{-18}{-18}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-12+6}{2\cdot(-9)}=\frac{-6}{-18}=\frac{1}{3}$$
Krok 3. Szkicowanie wykresu paraboli.
Współczynnik \(a\) był ujemny, więc parabola będzie mieć ramiona skierowane do dołu. Zaznaczamy na osi wyliczone przed chwilą miejsca zerowe (z pustymi kropkami, bo w nierówności wystąpił znak \(\lt\)).
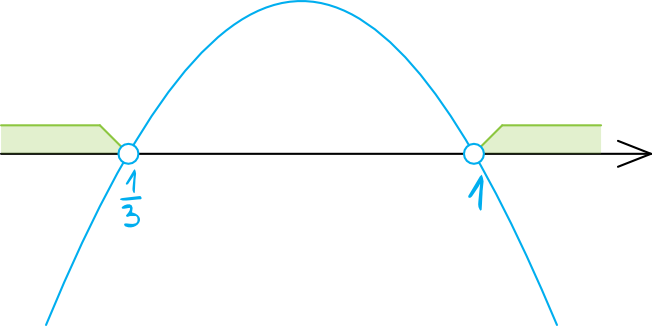
Szukamy argumentów dla których funkcja przyjmuje wartości mniejsze od zera, a więc interesować nas będzie suma przedziałów:
$$x\in\left(-\infty;\frac{1}{3}\right)\cup(1;+\infty)$$