Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W rysunku pomocniczym najważniejsze jest to, by zaznaczyć poprawnie kąt nachylenia ściany bocznej do płaszczyzny podstawy. Kiedy naniesiemy na rysunek dane z treści zadania, to otrzymamy taką oto sytuację:
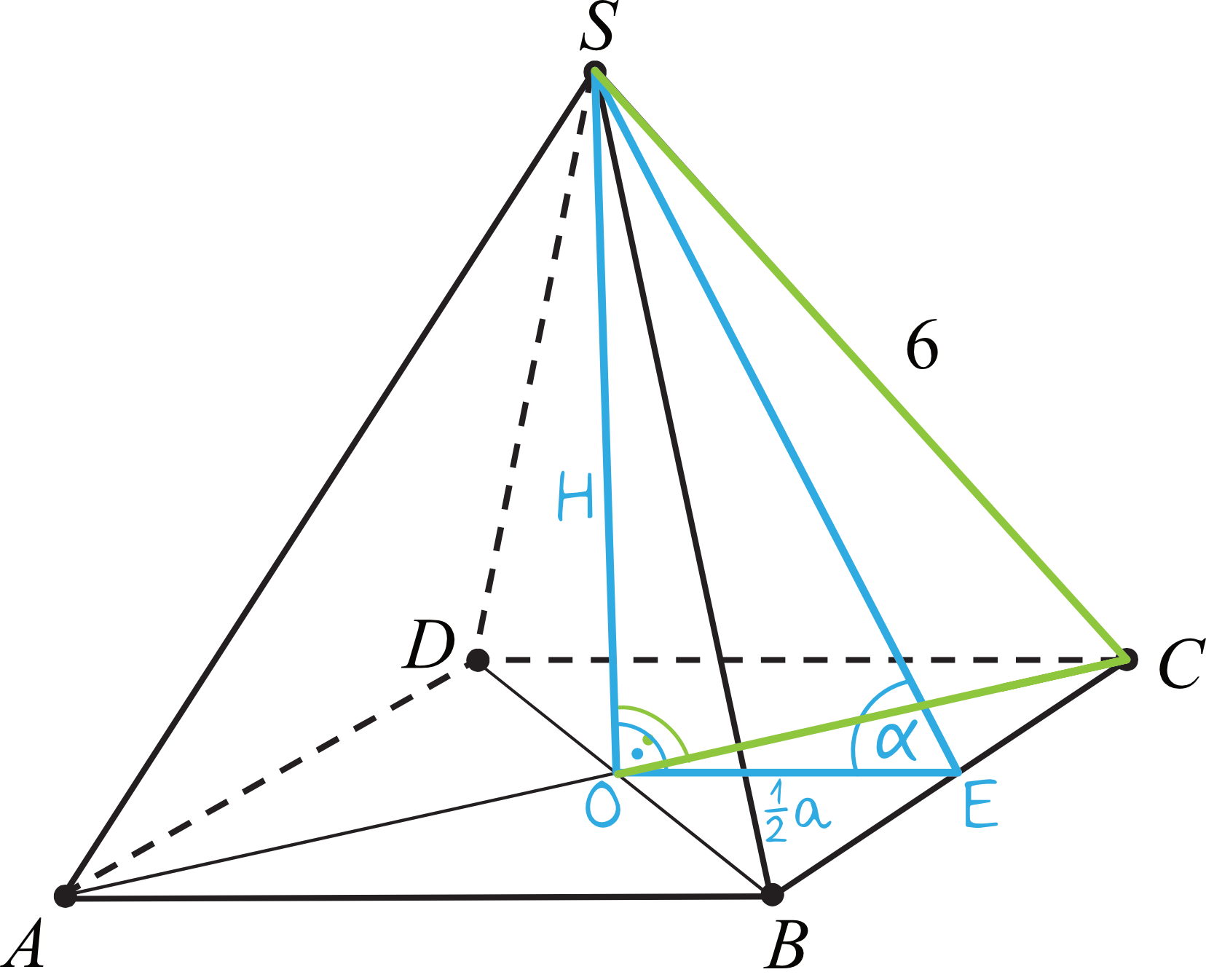
Kluczem do sukcesu jest dostrzeżenie przede wszystkim niebieskiego trójkąta prostokątnego \(SOE\) w którym dolna przyprostokątna jest połową długości krawędzi podstawy, boczna przyprostokątna jest wysokością bryły, a przeciwprostokątna jest wysokością ściany bocznej.
Krok 2. Wprowadzenie oznaczeń, które wynikają z informacji na temat tangensa.
Spójrzmy na niebieski trójkąt prostokątny \(SOE\). Wiemy, że \(tgα=\sqrt{7}\). Tangens jest to stosunek długości przyprostokątnej leżącej naprzeciwko kąta \(α\) względem przyprostokątnej leżącej przy tym kącie. I tu pojawia się problem, bo nie znamy ani jednej, ani drugiej długości. Zastanówmy się jednak co się musi stać, aby tangens naszego kąta \(α\) był równy \(\sqrt{7}\). Aby tak się stało, to przyprostokątna leżąca naprzeciwko kąta \(α\) (czyli nasza wysokość ostrosłupa) musi być \(\sqrt{7}\) razy większa od przyprostokątnej leżącej przy kącie \(α\). Jeżeli więc dolna przyprostokątna leżąca przy kącie \(α\) ma długość \(\frac{1}{2}a\), to wtedy wysokość naszej bryły będzie miała długość \(\sqrt{7}\cdot\frac{1}{2}a=\frac{a\sqrt{7}}{2}\).
Krok 3. Obliczenie długości krawędzi podstawy.
Spójrzmy teraz na zielony trójkąt prostokątny \(SOC\). Ten trójkąt w dolnej przyprostokątnej ma połowę długości przekątnej kwadratu, jego boczną przyprostokątną jest wysokość bryły, a przeciwprostokątną jest krawędź boczna o długości \(6\).
Z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\), czyli przyprostokątna \(OC\) będzie mieć długość \(\frac{a\sqrt{2}}{2}\). Wiemy też, że wysokość ostrosłupa jest równa \(H=\frac{a\sqrt{7}}{2}\). Skoro tak, to korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$\left(\frac{a\sqrt{2}}{2}\right)^2+\left(\frac{a\sqrt{7}}{2}\right)^2=6^2 \\
\frac{2a^2}{4}+\frac{7a^2}{4}=36 \\
\frac{9a^2}{4}=36 \\
9a^2=144 \\
a^2=16 \\
a=4 \quad\lor\quad a=-4$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(a=4\).
Krok 4. Obliczenie wysokości ostrosłupa.
Wiemy, że ostrosłup ma długość \(H=\frac{a\sqrt{7}}{2}\), zatem skoro \(a=4\), to:
$$H=\frac{4\sqrt{7}}{2}=2\sqrt{7}$$
Krok 5. Obliczenie objętości ostrosłupa.
Na koniec została już tylko formalność, bowiem skoro \(a=4\) oraz \(H=2\sqrt{7}\), to objętość ostrosłupa będzie równa:
$$V=\frac{1}{3}a^2\cdot H \\
V=\frac{1}{3}\cdot4^2\cdot2\sqrt{7} \\
V=\frac{1}{3}\cdot16\cdot2\sqrt{7} \\
V=\frac{32\sqrt{7}}{3}$$