Dany jest kwadrat o boku a=6. W ten kwadrat wpisano trójkąt równoboczny w ten sposób, że jeden wierzchołek

Dany jest kwadrat o boku $a=6$. W ten kwadrat wpisano trójkąt równoboczny w ten sposób, że jeden wierzchołek trójkąta jest wierzchołkiem kwadratu, a przeciwległy bok trójkąta jest równoległy do przekątnej kwadratu (patrz rysunek). Wykaż, że bok trójkąta jest równy $6(\sqrt{6}-\sqrt{2})$.

Rozwiązanie

Krok 1. Sporządzenie rysunku pomocniczego.
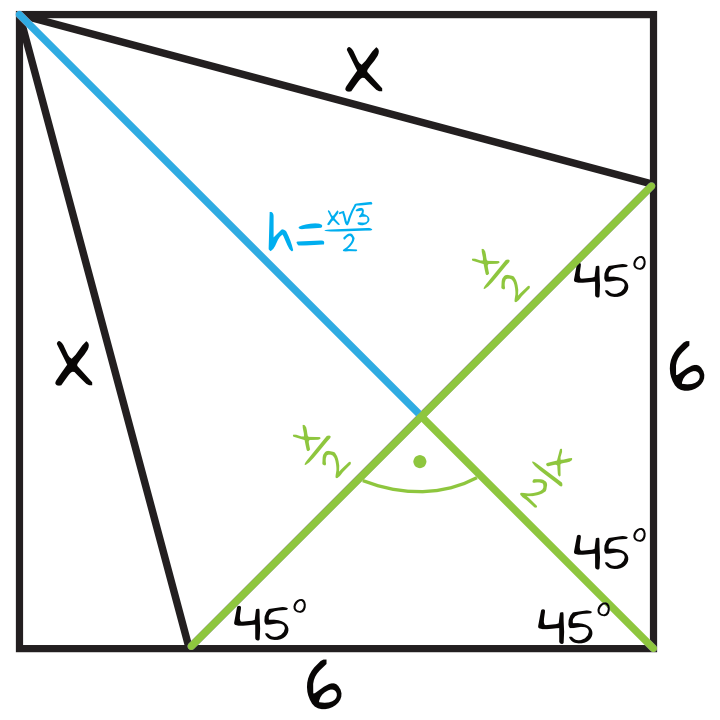
Jeżeli dorysujemy przekątną kwadratu, to pamiętając że przekątna kwadratu dzieli nam kąt prosty na dwa kąty po $45°$, otrzymamy następującą sytuację:

matura z matematyki

Krok 2. Zapisanie i rozwiązanie równania.
Kwadrat o boku $6$ ma długość przekątnej równą $6\sqrt{2}$. Patrząc się na rysunek widzimy, że ta przekątna składa się z wysokości trójkąta $\frac{x\sqrt{3}}{2}$ oraz połowy boku trójkąta $\frac{x}{2}$, zatem:
$$\frac{x\sqrt{3}}{2}+\frac{x}{2}=6\sqrt{2} \quad\bigg/\cdot2 \\
x\sqrt{3}+x=12\sqrt{2} \\
x(\sqrt{3}+1)=12\sqrt{2} \\
x=\frac{12\sqrt{2}}{\sqrt{3}+1} \\
x=\frac{12\sqrt{2}\cdot(\sqrt{3}-1)}{(\sqrt{3}+1)\cdot(\sqrt{3}-1)} \\
x=\frac{12\sqrt{2}\cdot(\sqrt{3}-1)}{3-1} \\
x=\frac{12\sqrt{2}\cdot(\sqrt{3}-1)}{2} \\
x=6\sqrt{2}\cdot(\sqrt{3}-1) \\
x=6\cdot(\sqrt{6}-\sqrt{2})$$

Odpowiedź

Wykazano dorysowując przekątną kwadratu.