Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczmy w układzie współrzędnych wskazane punkty i spróbujmy wskazać przybliżoną pozycję punktu \(C\), tak aby powstał nam kąt \(90°\).
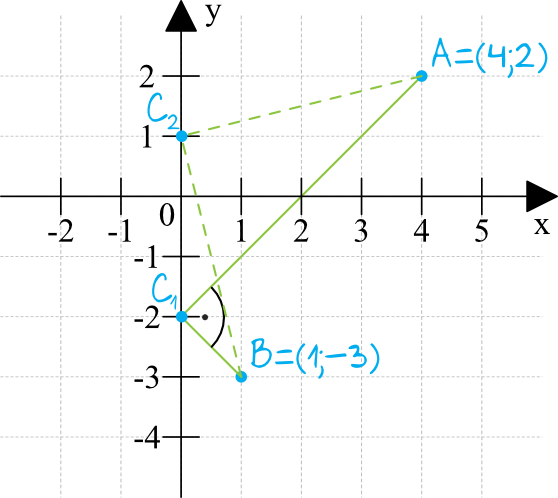
Ten konkretny rysunek już nam nieco zdradza, że będą dwa rozwiązania tego zadania, aczkolwiek nic się nie stanie kiedy nasz szkic uwzględni tylko jedną opcję (wszystko i tak wyjdzie w trakcie liczenia). Sam rysunek ma nam tylko przybliżyć omawianą sytuację.
To co jest bardzo ważne i co powinno wynikać ze szkicu, to fakt że punkt \(C\) jest na osi \(OY\), a skoro tak, to jedną z jego współrzędnych już znamy i jest to \(x=0\). Możemy nawet zapisać, że \(C=(0;y)\). W związku z tym musimy tak naprawdę policzyć tylko współrzędną igrekową tego punktu, która w dalszej części zadania będzie oznaczana właśnie symbolem \(y\).
Krok 2. Wyznaczenie współczynników kierunkowych prostej \(AC\) oraz \(BC\).
Korzystając ze wzoru na współczynnik kierunkowy prostej przechodzącej przez dwa punkty możemy zapisać, że:
$$a_{AC}=\frac{y_{C}-y_{A}}{x_{C}-x_{A}} \\
a_{AC}=\frac{y-2}{0-4} \\
a_{AC}=\frac{y-2}{-4}$$
$$a_{BC}=\frac{y_{C}-y_{B}}{x_{C}-x_{B}} \\
a_{BC}=\frac{y-(-3)}{0-1} \\
a_{BC}=\frac{y+3}{-1}$$
Krok 3. Ułożenie i rozwiązanie równania.
Skoro proste \(AC\) oraz \(BC\) przecinają się pod kątem prostym, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). W związku z tym:
$$a_{AC}\cdot a_{BC}=-1 \\
\frac{y-2}{-4}\cdot\frac{y+3}{-1}=-1 \\
\frac{(y-2)\cdot(y+3)}{4}=-1 \\
(y-2)\cdot(y+3)=-4 \\
y^2+3y-2y-6=-4 \\
y^2+y-2=0$$
Krok 4. Rozwiązanie powstałego równania kwadratowego.
Powstało nam równanie kwadratowe, zatem:
Współczynniki: \(a=1,\;b=1,\;c=-2\)
$$Δ=b^2-4ac=1^2-4\cdot1\cdot(-2)=1-(-8)=1+8=9 \\
\sqrt{Δ}=\sqrt{9}=3$$
$$y_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-1-3}{2\cdot1}=\frac{-4}{2}=-2 \\
y_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-1+3}{2\cdot1}=\frac{2}{2}=1$$
Krok 5. Analiza otrzymanego wyniku i zapisanie rozwiązania zadania.
Otrzymaliśmy dwie możliwości współrzędnej igrekowej punktu \(C\). Żadnej z nich nie możemy odrzucić, a to oznacza, że to zadanie ma dwa rozwiązania:
$$C=(0;-2) \quad\lor\quad C=(0;1)$$