Dana jest funkcja kwadratowa \(f(x)=-2(x+5)(x-11)\). Wskaż maksymalny przedział, w którym funkcja \(f\) jest rosnąca:
\((-\infty;3\rangle\)
\((-\infty;5\rangle\)
\((-\infty;11\rangle\)
\(\langle6;+\infty)\)
Rozwiązanie:
Krok 1. Obliczenie miejsc zerowych funkcji.
Z postaci iloczynowej w bardzo łatwy sposób jesteśmy w stanie określić miejsca zerowe tej funkcji, przyrównując \(-2(x+5)(x-11)\) do zera:
$$-2(x+5)(x-11)=0 \\
x+5=0 \quad\lor\quad x-11=0 \\
x_{1}=-5 \quad\lor\quad x_{2}=11$$
Krok 2. Obliczenie współrzędnej \(x\) wierzchołka paraboli.
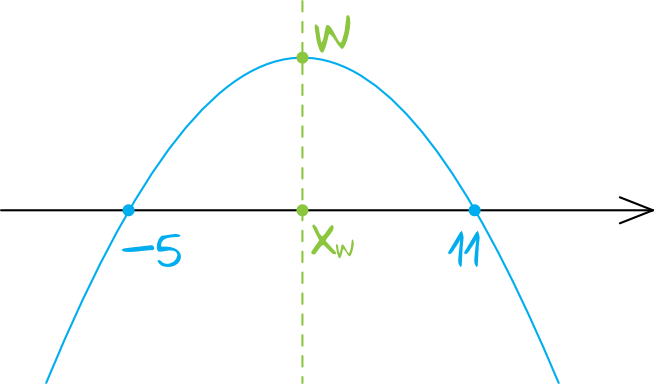
Nasza funkcja zapisana w postaci ogólnej miałaby ujemny współczynnik \(a=-2\) stąd też jej ramiona będą skierowane do dołu. Aby określić przedział w którym funkcja będzie rosnąca potrzebujemy znać jeszcze współrzędną \(x\) wierzchołka tej paraboli. Obliczymy ją w następujący sposób:
$$x_{W}=\frac{x_{1}+x_{2}}{2}=\frac{-5+11}{2}=\frac{6}{2}=3$$
To oznacza, że funkcja rośnie w przedziale \((-\infty;3\rangle\).
Odpowiedź:
A. \((-\infty;3\rangle\)

