Rozwiązanie
Krok 1. Potraktowanie ciągu jako funkcji.
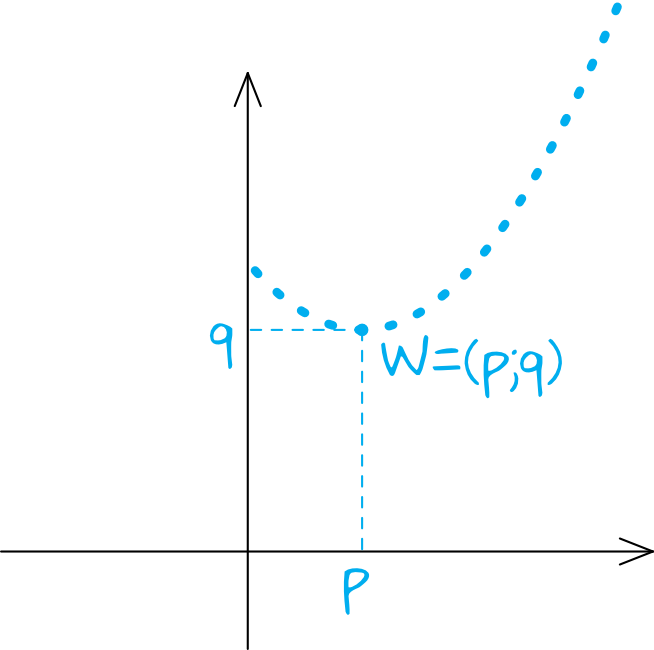
Potraktujmy nasz ciąg jak funkcję, która jest określona jedynie dla argumentów będących liczbami naturalnymi. Funkcja swoją najmniejszą lub największą wartość przyjmuje w wierzchołku \(W=(p;q)\). To oznacza, że tak naprawdę interesować nas będzie poznanie współrzędnych wierzchołka paraboli, ale z zastrzeżeniem, że współrzędna \(p\) musi być liczbą naturalną.
Krok 2. Wyznaczenie współrzędnej \(p\).
Współrzędną \(p\) obliczymy ze wzoru:
$$p=\frac{-b}{2a}$$
Ze wzoru ciągu możemy odczytać, że \(b=-24\) oraz \(a=\frac{3}{4}\). W związku z tym:
$$p=\frac{-(-24)}{2\cdot\frac{3}{4}} \\
p=\frac{24}{\frac{3}{2}} \\
p=24:\frac{3}{2} \\
p=24\cdot\frac{2}{3} \\
p=16$$
Współrzędna \(p\) jest liczbą naturalną i to jest bardzo dobra wiadomość, bo za chwilę będziemy mogli podstawić tę liczbę do wzoru naszego ciągu. Gdyby się okazało, że \(p\) jest równe np. \(16\frac{1}{5}\), to w kolejnym kroku musielibyśmy sprawdzić wartość funkcji dla argumentów \(n=16\) oraz \(n=17\).
Krok 3. Wyznaczenie współrzędnej \(q\).
Współrzędną \(q\) moglibyśmy wyznaczyć ze wzoru \(q=\frac{-Δ}{4a}\), ale skoro znamy wartość współrzędnej \(p=16\) to możemy po prostu podstawić do wzoru wartość \(n=16\) i w ten sposób obliczymy wartość przyjmowaną w tym wierzchołku, czyli wartość współrzędnej \(q\). Zatem:
$$q=\frac{3}{4}\cdot16^2-24\cdot16+90 \\
q=\frac{3}{4}\cdot256-384+90 \\
q=\frac{3}{4}\cdot256-384+90 \\
q=192-384+90 \\
q=-102$$
To oznacza, że najmniejszą wartością przyjmowaną przez ten ciąg jest wartość \(16\)-stego wyrazu i jest ona równa \(-102\).