Odcinki \(BC\) i \(DE\) są równoległe i \(|AE|=4\), \(|DE|=3\) (zobacz rysunek). Punkt \(D\) jest środkiem odcinka \(AB\). Długość odcinka \(BC\) jest równa:
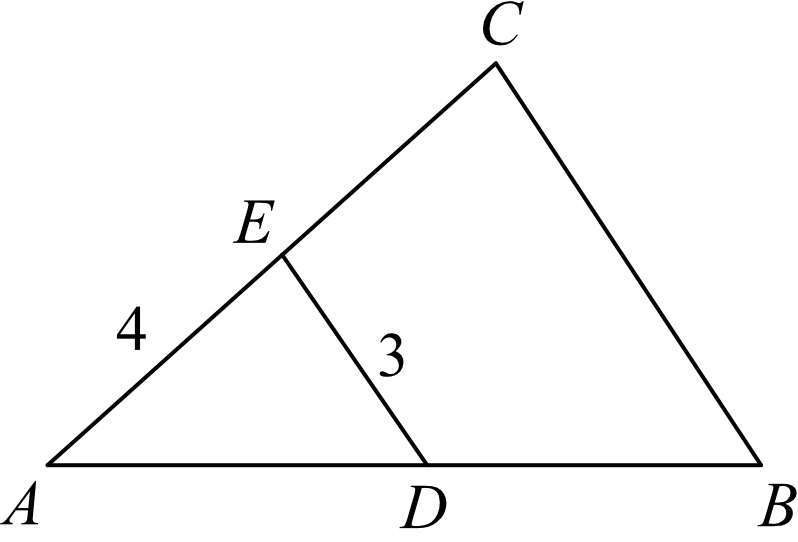
Z treści zadania wynika, że \(|AD|=|DB|\), bo punkt \(D\) jest środkiem odcinka \(AB\). Skoro przez ten punkt \(D\) jest poprowadzona prosta równoległa do boku \(BC\), to podobna prawidłowość zajdzie także na odcinku \(AC\), gdzie punkt \(E\) jest w takim razie także środkiem tego odcinka. W związku z tym \(|AE|=|EC|=4\).
Znając długość odcinka \(EC\) możemy obliczyć miarę odcinka \(AC\):
$$|AC|=|AE|+|EC|=4+4=8$$
Trójkąty \(ADE\) oraz \(ABC\) są trójkątami podobnymi. Skąd to wiemy? Wynika to z cechy kąt-kąt-kąt, bo obydwa trójkąty mają wspólny kąt \(CAB\) oraz wiemy że \(|\sphericalangle ADE|=|\sphericalangle ABC|\), gdyż są to tak naprawdę kąty odpowiadające.
Skoro tak, to możemy ułożyć następujące równanie:
$$\frac{|DE|}{|AE|}=\frac{|BC|}{|AC|} \\
\frac{3}{4}=\frac{|BC|}{8} \quad\bigg/\cdot8 \\
|BC|=\frac{24}{4} \\
|BC|=6$$
B. \(6\)

