Funkcja liniowa f(x)=ax+b jest malejąca i ma ujemne miejsce zerowe. Dla takiej funkcji prawdziwa jest nierówność

Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować sobie omawianą sytuację:


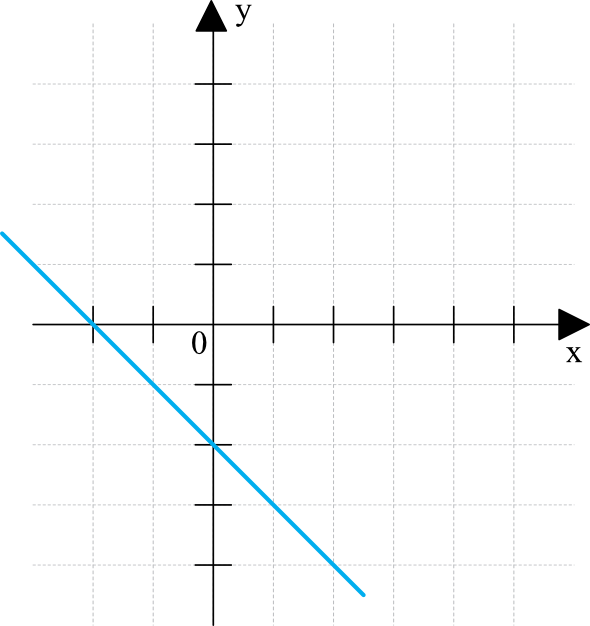
Krok 2. Odczytanie wartości współczynników \(a\) oraz \(b\)
Funkcja jest malejąca, zatem współczynnik \(a\) jest liczbą ujemną, czyli \(a\lt0\).
Współczynnik \(b\) mówi nam o miejscu przecięcia się wykresu z osią igreków. Widzimy wyraźnie, że funkcja przecina oś igreków w ujemnej wartości, czyli \(b\lt0\).

Krok 3. Wybór prawidłowej odpowiedzi.
Wiemy już, że zarówno \(a\) jak i \(b\) są liczbami ujemnymi. Przeanalizujmy teraz każdą z odpowiedzi:
Odp. A. \(a+b\gt0\) - to nie może być prawda, bo suma dwóch liczb ujemnych na pewno będzie mniejsza od zera.
Odp. B. \(a+b\lt0\) - to prawda, bo suma dwóch liczb ujemnych na pewno będzie mniejsza od zera.
Odp. C. \(ab=0\) - to nie jest prawda, bo iloczyn dwóch liczb ujemnych da wynik dodatni.
Odp. D. \(ab\lt0\) - to nie jest prawda, bo iloczyn dwóch liczb ujemnych da wynik dodatni.