Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Kluczem do sukcesu będzie dorysowanie promienia \(OB\), który zgodnie z własnościami stycznych do okręgu, będzie tworzył ze styczną kąt prosty:
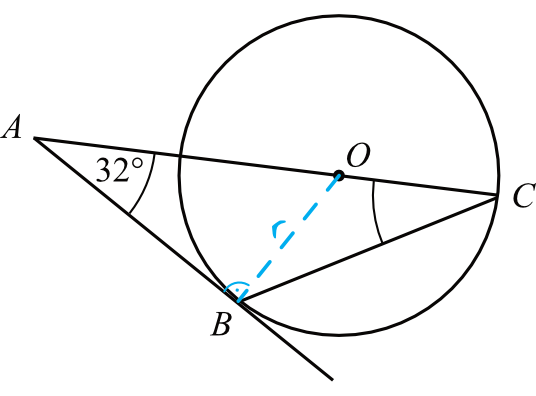
Krok 2. Obliczenie miary kąta \(AOB\).
Spójrzmy na trójkąt \(ABO\). Znamy tutaj miary dwóch kątów, zatem trzeci brakujący kąt będzie miał miarę:
$$|\sphericalangle AOB|=180°-90°-32°=58°$$
Krok 3. Obliczenie miary kąta \(BOC\).
Kąt \(AOB\) oraz kąt \(BOC\) to kąty przyległe, zatem łączna ich miara jest równa \(180°\). Skoro tak, to:
$$|\sphericalangle BOC|=180°-58°=122°$$
Krok 4. Obliczenie miary kąta \(ACB\).
Spójrzmy na trójkąt \(BCO\). Jest to trójkąt równoramienny, ponieważ ramiona \(BO\) oraz \(CO\) mają długość promienia. Z własności takich trójkątów wiemy, że kąty przy podstawie mają jednakową miarę. Skoro więc kąt między ramionami ma miarę \(122°\), to na dwa kąty przy podstawie zostanie nam:
$$180°-122°=58°$$
Kąty przy podstawie mają mieć równą miarę, zatem kąt \(BCO\) (czyli \(ACB\)), ma miarę:
$$|\sphericalangle ACB|=58°:2=29°$$