Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zgodnie z treścią zadania mamy następujące dwie figury
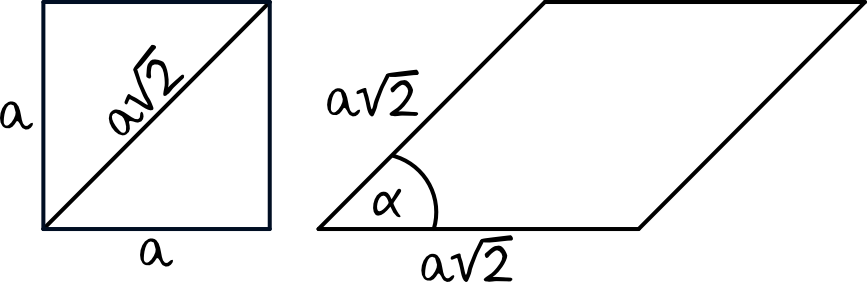
Krok 2. Zapisanie pól powierzchni obydwu figur.
Pole kwadratu jest równe:
$$P_{k}=a^2$$
Pole rombu jest równe:
$$P_{r}=a\sqrt{2}\cdot a\sqrt{2}\cdot sinα \\
P_{r}=2a^2\cdot sinα$$
Krok 3. Obliczenie miary kąta \(α\).
Z treści zadania wynika, że pola kwadratu oraz rombu są sobie równe, zatem:
$$P_{k}=P_{r} \\
a^2=2a^2\cdot sinα \\
1=2\cdot sinα \\
sinα=\frac{1}{2}$$
Z tablic matematycznych możemy odczytać, że sinus przyjmuje wartość \(\frac{1}{2}\) dla kąta \(30°\) i to jest też nasza końcowa odpowiedź.