Jedną z metod obliczania wartości funkcji trygonometrycznych jest wykorzystanie układu współrzędnych i zależności jakie tam się pojawiają. Narysujmy kąt alfa w taki sposób, by jedno z jego ramion pokrywało się z osią iksów, a wierzchołek trójkąta znajdował się w początku układu współrzędnych. Na drugim ramieniu oznaczymy sobie punkt \(P\) o współrzędnych \((x;y)\), który jest odległy o \(r\) od początku układu współrzędnych.
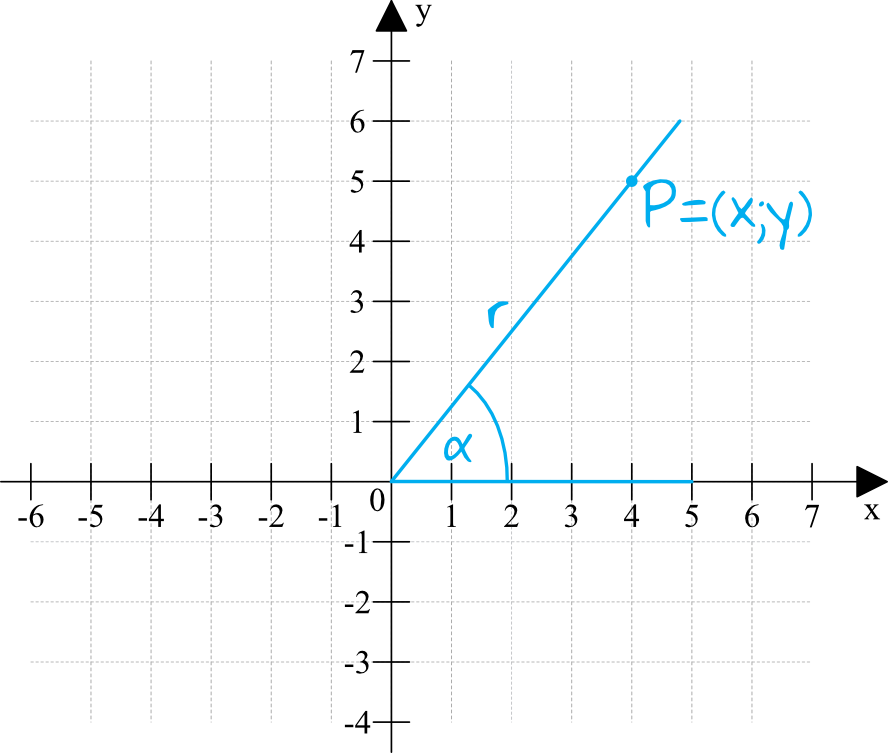
Okazuje się, że zgodnie z oznaczeniami na powyższym rysunku:
$$sinα=\frac{y}{r} \\
cosα=\frac{x}{r} \\
tgα=\frac{y}{x} \\
\quad \\
r=\sqrt{x^2+y^2}$$
To oznacza, że znając współrzędne punktu \(P\) oraz odległość \(r\) jesteśmy w stanie obliczyć wartości poszczególnych funkcji trygonometrycznych. Zazwyczaj zadania z wykorzystaniem tej własności polegają na tym, że mamy podane współrzędne punktu \(P\), samodzielnie musimy obliczyć długość \(r\) (korzystając z podanego powyżej wzoru lub stosując Twierdzenie Pitagorasa) i w ten sposób możemy wyznaczyć wartości interesujących nas funkcji. Spójrzmy na przykładowe zadanie:
Możemy nawet całą sytuację przedstawić na rysunku pomocniczym:
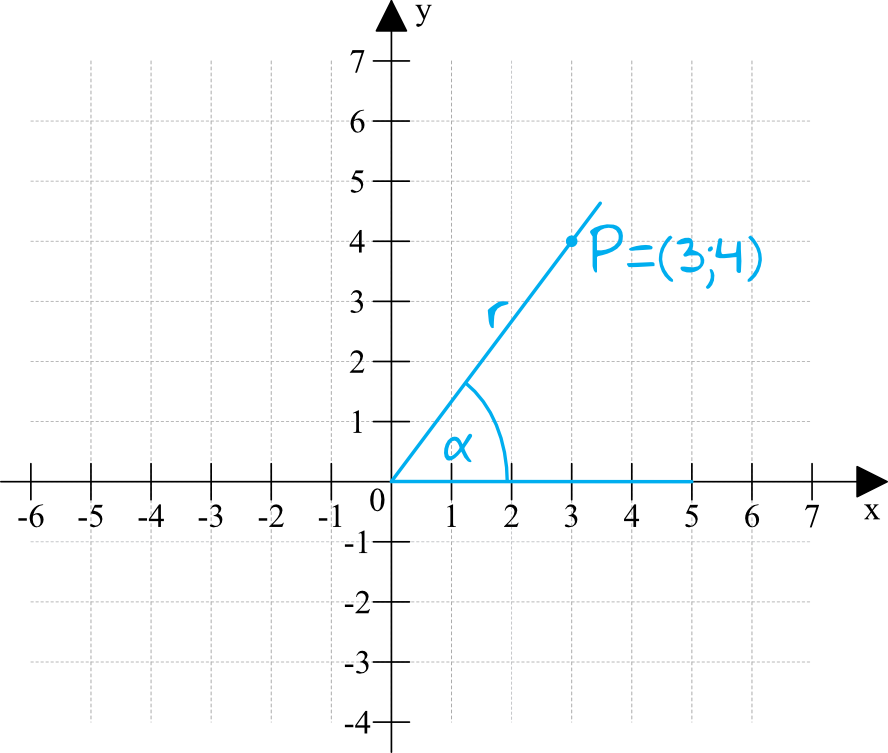
W tym zadaniu na pewno wykorzystamy wzór:
$$sinα=\frac{y}{r}$$
Współrzędną igrekową znamy, jest to \(y=4\). Brakuje nam długości \(r\). Jak ją wyliczymy? Możemy skorzystać z podanego wzoru \(r=\sqrt{x^2+y^2}\) lub też możemy dostrzec pewien trójkąt prostokątny i wyznaczyć tę długość z Twierdzenia Pitagorasa (pokażemy sobie oba sposoby).
Krok 1. Wyznaczenie długości \(r\).
Wyznaczając \(r\) za pomocą wzoru otrzymamy:
$$r=\sqrt{x^2+y^2} \\
r=\sqrt{3^2+4^2} \\
r=\sqrt{9+16} \\
r=\sqrt{25} \\
r=5$$
Jeżeli nie pamiętamy tego wzoru, to możemy zastosować Twierdzenie Pitagorasa (z którego zresztą ten wzór się wywodzi):
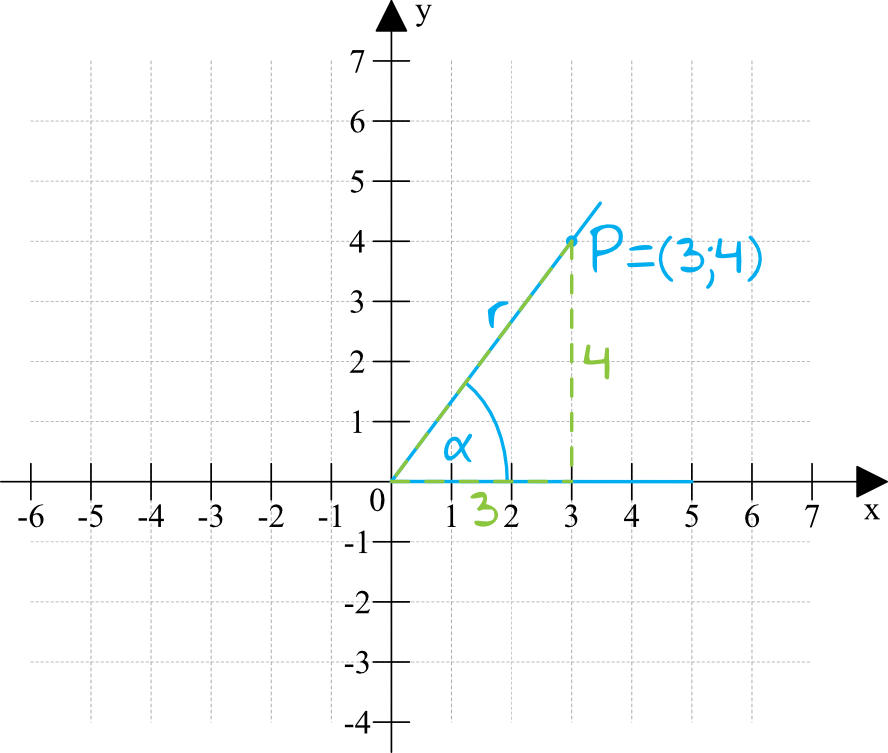
Korzystając z własności powyższego trójkąta prostokątnego możemy zapisać, że:
$$3^2+4^2=r^2 \\
9+16=r^2 \\
r^2=25 \\
r=5 \lor r=-5$$
Wartość ujemną oczywiście odrzucamy (bo długość nie może być ujemna), zatem \(r=5\).
Krok 2. Wyznaczenie wartości \(sinα\).
Znamy już wszystkie potrzebne dane, zatem możemy wyznaczyć wartość sinusa:
$$sinα=\frac{y}{r}=\frac{4}{5}$$
I tu także zacznijmy od rysunku pomocniczego:
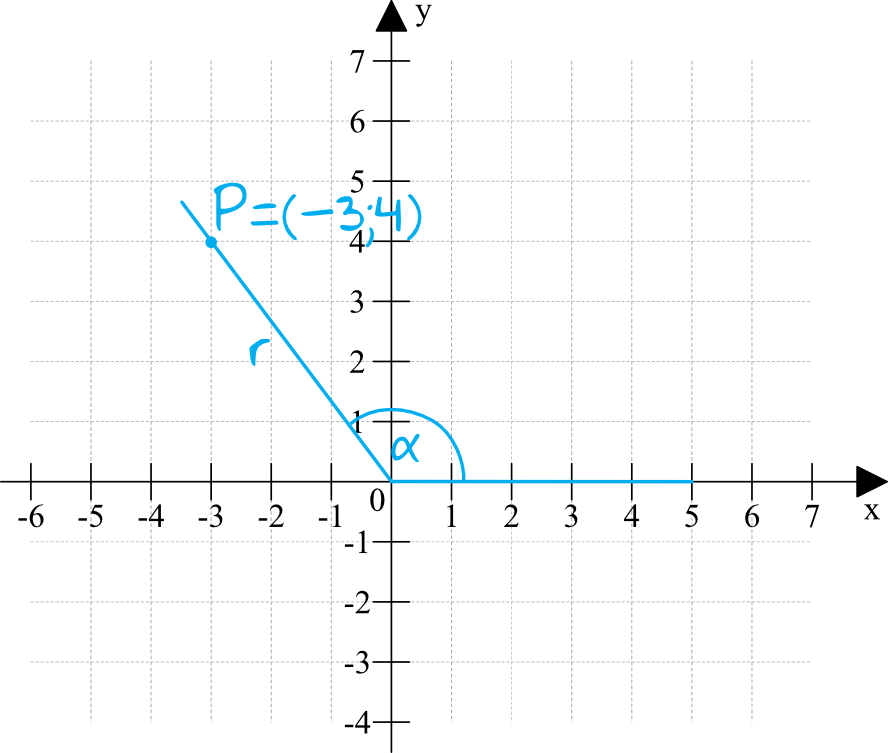
Zadanie jest bardzo podobne do poprzedniego, z tą jednak różnicą iż tym razem powstał nam kąt rozwarty, bo współrzędna iksowa jest ujemna, no i teraz musimy podać wartość cosinusa. Czy coś zmienia się w toku naszych obliczeń? Zupełnie nic, nadal musimy obliczyć najpierw długość \(r\), a następnie wyznaczymy sobie poszukiwaną wartość cosinusa.
Krok 1. Wyznaczenie długości \(r\).
Korzystając ze wzoru na długość \(r\) otrzymamy:
$$r=\sqrt{x^2+y^2} \\
r=\sqrt{(-3)^2+4^2} \\
r=\sqrt{9+16} \\
r=\sqrt{25} \\
r=5$$
Krok 2. Wyznaczenie wartości \(cosα\).
Zgodnie ze wzorami:
$$cosα=\frac{x}{r}$$
Skoro znamy już długość \(r\), znamy też współrzędną iksową \(x=-3\) to możemy zapisać, że:
$$cosα=\frac{-3}{5}=-\frac{3}{5}$$
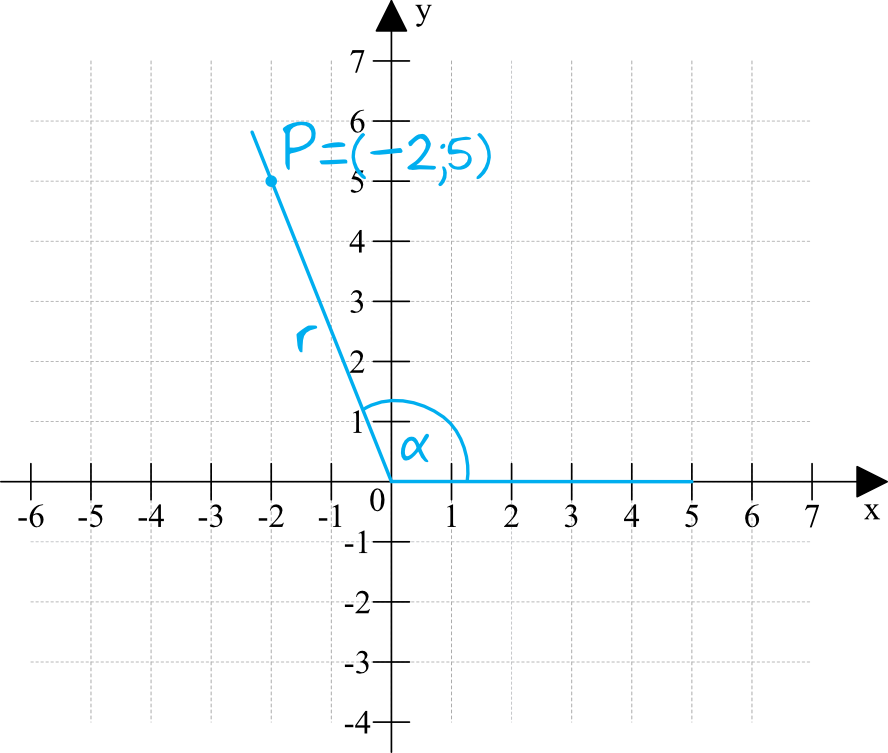
Zdecydowanie najprostsze jest wyznaczanie wartości tangensa, bowiem tutaj zgodnie ze wzorem \(tgα=\frac{y}{x}\) musimy podstawić tylko i wyłącznie współrzędne naszego punktu \(P\). Nie ma więc tym razem konieczności wyliczania długości \(r\). Możemy zatem zapisać, że:
$$tgα=\frac{5}{-2}=-\frac{5}{2}$$
Z układem współrzędnych, a raczej z jego ćwiartkami, związana jest jeszcze jedna własność, która dotyczy określania znaków poszczególnych funkcji trygonometrycznych. Okazuje się, że po tym w której ćwiartce znajduje się ramię naszego kąta możemy określić czy wartość funkcji trygonometrycznej jest dodatnia czy ujemna.

To która funkcja przyjmuje wartości dodatnie lub ujemne wynika bezpośrednio ze wzorów zapisanych na początku tematu. Po prostu tam gdzie w liczniku i mianowniku pojawi się jedna liczba dodatnia i jedna ujemna, tam wynik takiego dzielenia będzie po prostu ujemny. Taka sytuacja miała miejsce chociażby w drugim przykładzie – tam funkcja cosinus była ujemna, bo licznik był liczbą ujemną, a mianownik był dodatni. To samo stało się w trzecim przykładzie, tam licznik był dodatni, a mianownik ujemny.
Co nam ta wiedza daje? W ten oto sposób jesteśmy w stanie błyskawicznie stwierdzić czy dana funkcja trygonometryczna jest dodatnia, czy też ujemna (bez zaglądania do tablic). Przykładowo znając te zależności w układzie współrzędnych wiemy, że np. dla kątów rozwartych (czyli takich, których ramię znajdzie się w II ćwiartce) dodatnią wartość będzie mieć jedynie sinus. Pozostałe funkcje (cosinus oraz tangens) przyjmą wartości ujemne. Ta zasada wyjaśnia nam także dlaczego wszystkie funkcje trygonometryczne są dodatnie dla kątów ostrych (czyli takich, których ramię znajdzie się w I ćwiartce), bo po prostu współrzędna iksowa i igrekowa punktu na ramieniu takiego kąta będzie liczbą dodatnią.
Wiedza na temat tego kiedy funkcje przyjmują wartości dodatnie lub ujemne przydaje się przede wszystkim na poziomie rozszerzonym. Aby zapamiętać kiedy funkcje są dodatnie można posłużyć się prostym wierszykiem:
W pierwszej ćwiartce wszystkie są dodatnie
W drugiej tylko sinus
W trzeciej tangens i cotangens
A w czwartej cosinus
