Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczmy sobie w układzie współrzędnych nasze współrzędne i połączmy je, tworząc trójkąt \(ABC\).
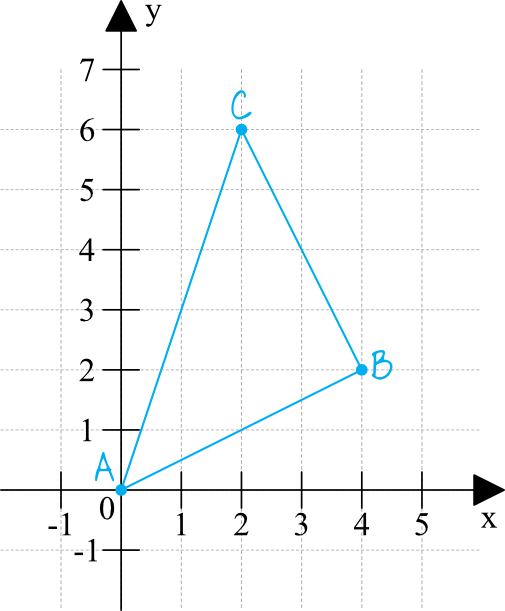
Obliczenie pola tego trójkąta w standardowy sposób może być nieco problematyczne. Kluczem do sukcesu jest dostrzeżenie, że nasz trójkąt jest prostokątny, więc wystarczyłoby poznać długości odcinków \(AB\) oraz \(BC\) i z nich wyliczyć pole powierzchni. Jednak tak prawdę mówiąc to gdyby chcieć uczciwie rozwiązać takie zadanie (np. gdyby to było zadanie otwarte) to najpierw trzeba byłoby udowodnić, że jest to trójkąt prostokątny, bo nie jest to takie oczywiste. W tym celu trzeba byłoby obliczyć wszystkie długości boków tego trójkąta (ze wzoru na długość odcinka o znanych współrzędnych) i z Twierdzenia Pitagorasa należałoby wykazać, że zachodzi równość \(a^2+b^2=c^2\), co byłoby dowodem na to, że trójkąt jest prostokątny.
Nie mniej jednak można podejść do zadania jeszcze prościej i przede wszystkim bezpieczniej. Możemy skorzystać z takiej oto prostej metody:
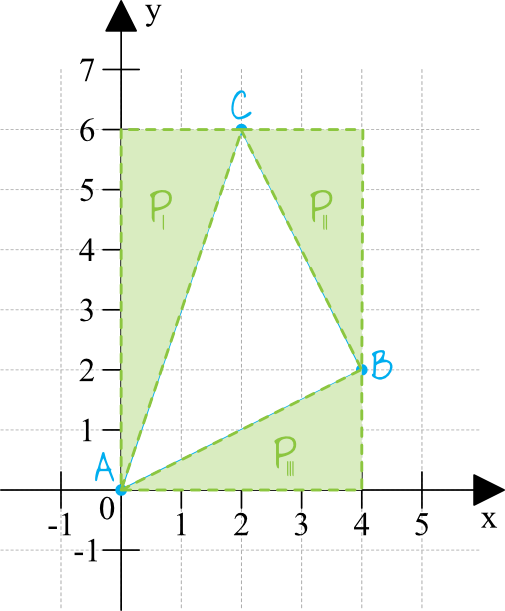
Pole naszego trójkąta \(ABC\) to będzie pole tego dużego prostokąta, pomniejszone o pola trójkąta I, II oraz III. Pola tych małych trójkątów są bardzo proste do policzenia, bo są to trójkąty prostokątne o znanych nam przyprostokątnych.
Krok 2. Obliczenie pola powierzchni małych trójkątów.
Pole trójkąta I:
\(P_{I}=\frac{1}{2}\cdot6\cdot2 \\
P_{I}=3\cdot2 \\
P_{I}=6\)
Pole trójkąta II:
\(P_{II}=\frac{1}{2}\cdot4\cdot2 \\
P_{II}=2\cdot2 \\
P_{II}=4\)
Pole trójkąta III:
\(P_{III}=\frac{1}{2}\cdot4\cdot2 \\
P_{III}=2\cdot2 \\
P_{III}=4\)
Krok 3. Wyznaczenie pola powierzchni trójkąta \(ABC\).
Nasz trójkąt \(ABC\) to będzie pole prostokąta o wymiarach \(4\times6\), pomniejszone o sumę pól małych trójkątów.
Pole prostokąta jest równe:
$$P_{pr}=4\cdot6 \\
P_{pr}=24$$
Suma pól małych trójkątów jest równa:
$$P_{I,II,III}=6+4+4 \\
P_{I,II,III}=14$$
W związku z tym pole trójkąta \(ABC\) jest równe:
$$P_{ABC}=24-14 \\
P_{ABC}=10$$