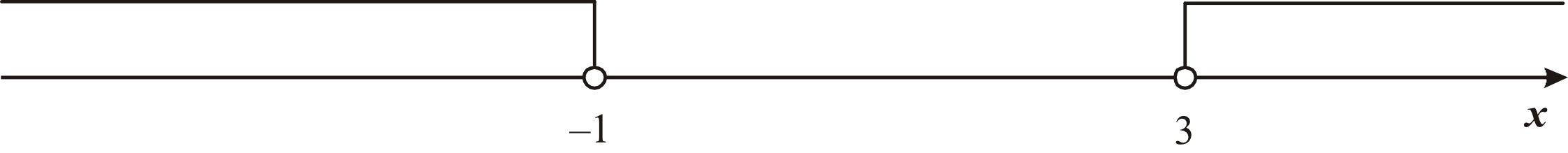Zbiór rozwiązań nierówności \((x+1)(x-3)\gt0\) przedstawiony jest na rysunku:


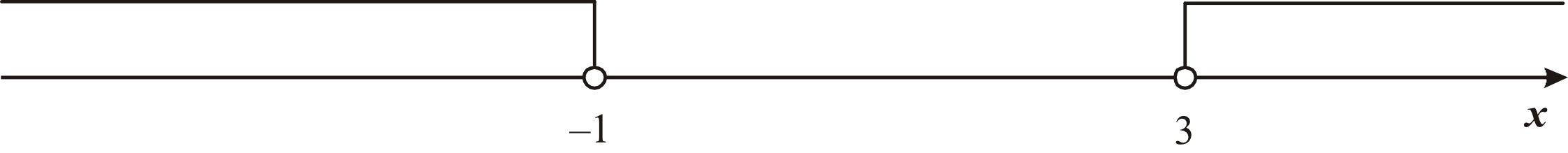
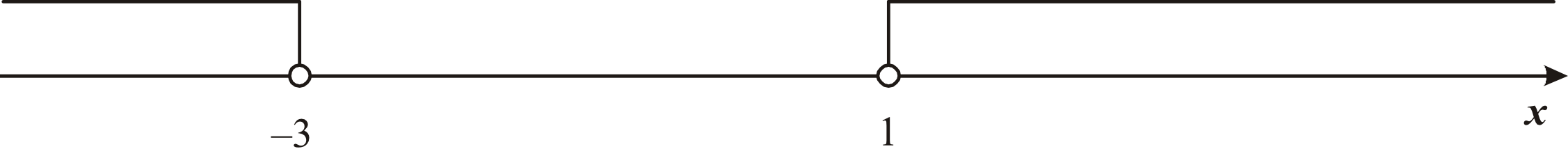
Aby wyznaczyć miejsca zerowe wystarczy przyrównać wielomian \((x+1)(x-3)\) do zera. Wielomian jest podany w postaci iloczynowej, co znacznie upraszcza ustalenie miejsc zerowych, bo tak naprawdę musimy przyrównać do zera wartości w każdym z nawiasów, zatem:
$$(x+1)(x-3)=0 \\
x+1=0 \quad\lor\quad x-3=0 \\
x=-1 \quad\lor\quad x=3$$
Ramiona paraboli będą na pewno skierowane do góry, bo po wymnożeniu wartości w nawiasach otrzymamy \(x^2\), czyli współczynnik \(a\gt0\). Zaznaczamy na osi wyliczone miejsca zerowe. Kropki będą niezamalowane, bo w nierówności wystąpił znak \(\gt\).

Poszukujemy wartości większych od zera, tak więc interesuje nas przedział \(x\in(-\infty;-1)\cup(3;+\infty)\). Taki zbiór został przedstawiony na trzecim rysunku i to jest nasza poszukiwana odpowiedź.