W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy:
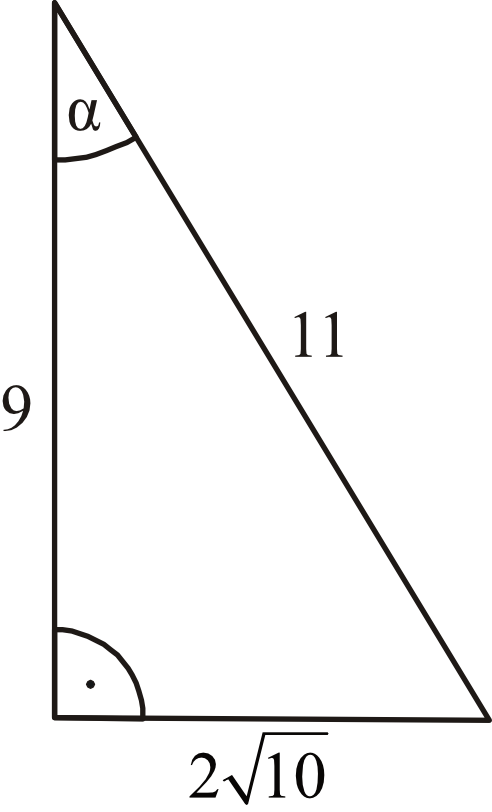
\(cosα=\frac{9}{11}\)
\(sinα=\frac{9}{11}\)
\(sinα=\frac{11}{2\sqrt{10}}\)
\(cosα=\frac{2\sqrt{10}}{11}\)
Rozwiązanie:
Krok 1. Obliczenie wartości sinusa.
Sinus kąta \(α\) to stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej.
$$sinα=\frac{2\sqrt{10}}{11}$$
Krok 2. Obliczenie wartości cosinusa.
Cosinus kąta \(α\) to stosunek długości przyprostokątnej leżącej przy tym kącie do długości przeciwprostokątnej.
$$cosα=\frac{9}{11}$$
Z tego wynika, że poprawne obliczenie wartości funkcji trygonometrycznej nastąpiło w odpowiedzi pierwszej.
Odpowiedź:
A. \(cosα=\frac{9}{11}\)

