W trójkącie równoramiennym \(ABC\) dane są \(|AC|=|BC|=5\) oraz wysokość \(|CD|=2\). Podstawa \(AB\) tego trójkąta ma długość:
\(6\)
\(2\sqrt{21}\)
\(2\sqrt{29}\)
\(14\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
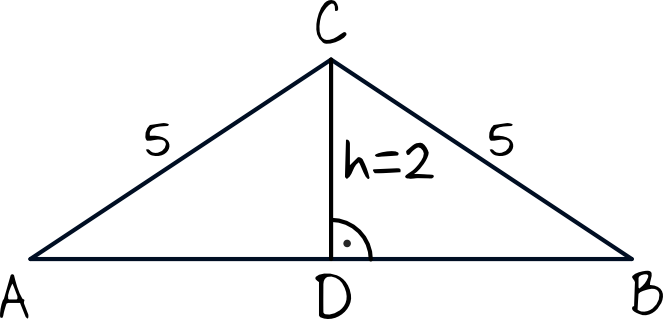
Analizując rysunek możemy wywnioskować, że aby obliczyć długość podstawy \(AB\) wystarczy z Twierdzenia Pitagorasa obliczyć długości odcinków \(AD\) oraz \(DB\). Wiemy też, że te odcinki będą równej długości (bo wysokość trójkąta równoramiennego dzieli jego podstawę na dwie równe części, zresztą widać to też wyraźnie z rysunku), więc wystarczy że obliczymy długość odcinka np. \(AD\) i pomnożymy ją przez \(2\).
Krok 2. Obliczenie długości odcinka \(AD\).
Zgodnie z Twierdzeniem Pitagorasa:
$$a^2+b^2=c^2 \\
a^2+2^2=5^2 \\
a^2+4=25 \\
a^2=21 \\
a=\sqrt{21}$$
Zatem \(|AD|=\sqrt{21}\).
Krok 3. Obliczenie długości odcinka \(AB\).
$$|AB|=2\cdot|AD|=2\cdot\sqrt{21}=2\sqrt{21}$$
Odpowiedź:
B. \(2\sqrt{21}\)

