Rozwiązanie
Krok 1. Dostrzeżenie, że boki \(EC\) oraz \(FC\) mają jednakową długość.
Spójrzmy na odcinki \(EC\) oraz \(FC\). Jeden i drugi to wysokości trójkątów równobocznych (\(ACD\) oraz \(ABC\)) o boku \(a=4cm\). To z kolei prowadzi nas do bardzo ważnego wniosku, że odcinki \(EC\) oraz \(FC\) są jednakowej długości (w dalszych krokach obliczymy sobie jaka jest to dokładnie długość). Póki co możemy zapisać, że \(|EC|=|FC|\). Mając tę informację wiemy już na pewno, że trójkąt \(EFC\) jest przynajmniej równoramienny (nie jesteśmy jeszcze pewni, czy jest równoboczny).
Krok 2. Dostrzeżenie, że kąt \(ECF\) ma miarę \(60°\).
Wysokość trójkąta równobocznego jest tak naprawdę dwusieczną kąta. Jeżeli więc spojrzymy np. na trójkąt \(ACD\), to stwierdzimy, że wysokość \(EC\) dzieli kąt przy wierzchołku \(C\) na dwa kąty o mierze \(30°\). Podobnie będzie w przypadku trójkąta \(ABC\). Na rysunku sytuacja będzie wyglądać następująco:
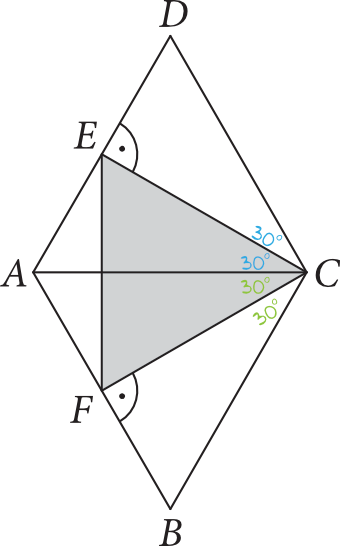
Możemy więc powiedzieć, że kąt \(ECF\) ma miarę \(60°\).
Krok 3. Zakończenie dowodzenia.
Wiemy już, że trójkąt jest przynajmniej równoramienny, bo ramiona \(EC\) oraz \(FC\) są jednakowej długości. Wiemy też, że kąt \(ECF\) ma miarę \(60°\). Z własności trójkątów równoramiennych wynika, że kąty przy podstawie mają jednakową miarę. U nas oznaczałoby to, że kąty przy podstawie \(EF\) muszą mieć łączną miarę \(180°-60°=120°\), a to oznacza, że każdy z kątów przy podstawie musi mieć miarę:
$$120°:2=60°$$
Wyszło nam więc, że każdy kąt trójkąta \(EFC\) ma miarę \(60°\), zatem jest to trójkąt równoboczny.
Krok 4. Obliczenie długości boków trójkąta \(EFC\).
Do obliczenia pola powierzchni potrzebujemy poznać długość boku trójkąta. Widzimy wyraźnie, że bok np. \(EC\) jest wysokością trójkąta równobocznego \(ACD\). Korzystając ze wzoru na wysokość trójkąta równobocznego możemy zapisać, że:
$$|EC|=\frac{a\sqrt{3}}{2} \\
|EC|=\frac{4\sqrt{3}}{2} \\
|EC|=2\sqrt{3}[cm]$$
To oznacza, że każdy bok naszego trójkąta \(EFC\) ma długość \(2\sqrt{3}cm\).
Krok 5. Obliczenie pola powierzchni trójkąta \(EFC\).
Wiemy już, że bok tego trójkąta ma długość \(2\sqrt{3}cm\), zatem podstawiając te dane do wzoru na pole trójkąta równobocznego otrzymamy:
$$P=\frac{a^2\sqrt{3}}{4} \\
P=\frac{(2\sqrt{3})^2\sqrt{3}}{4} \\
P=\frac{4\cdot3\cdot\sqrt{3}}{4} \\
P=3\sqrt{3}[cm^2]$$