Tworząca stożka ma długość \(l\), a promień jego podstawy jest równy \(r\).
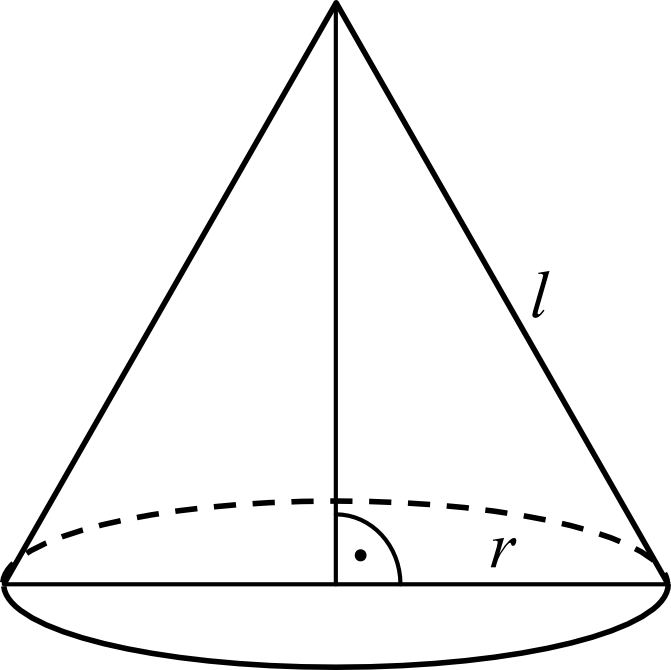
Powierzchnia boczna tego stożka jest \(2\) razy większa od pola jego podstawy. Wówczas:
\(r=\frac{1}{6}l\)
\(r=\frac{1}{4}l\)
\(r=\frac{1}{3}l\)
\(r=\frac{1}{2}l\)
Rozwiązanie:
Krok 1. Ułożenie poprawnego równania na podstawie danych z treści zadania.
Skoro powierzchnia boczna stożka (określana wzorem \(πrl\)) jest \(2\) razy większa od pola podstawy (określanego wzorem \(πr^2\)), to znaczy że prawdziwe jest równanie:
$$πrl=2\cdot πr^2$$
(Mnożymy przez \(2\) pole podstawy by było one równe polu ściany bocznej.)
Krok 2. Wyznaczenie wartości \(r\).
Na podstawie zapisanego równania możemy wyznaczyć długość promienia \(r\), zatem:
$$πrl=2\cdot πr^2 \quad\bigg/:π \\
rl=2r^2 \quad\bigg/:r \\
l=2r \\
r=\frac{1}{2}l$$
Odpowiedź:
D. \(r=\frac{1}{2}l\)

