Prostokąt \(ABCD\) o przekątnej długości \(2\sqrt{13}\) jest podobny do prostokąta o bokach długości \(2\) i \(3\). Obwód prostokąta \(ABCD\) jest równy:
\(10\)
\(20\)
\(5\)
\(24\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego i obliczenie długości przekątnej mniejszego prostokąta.
Zgodnie z treścią zadania nasze prostokąty będą wyglądać mniej więcej w ten sposób:
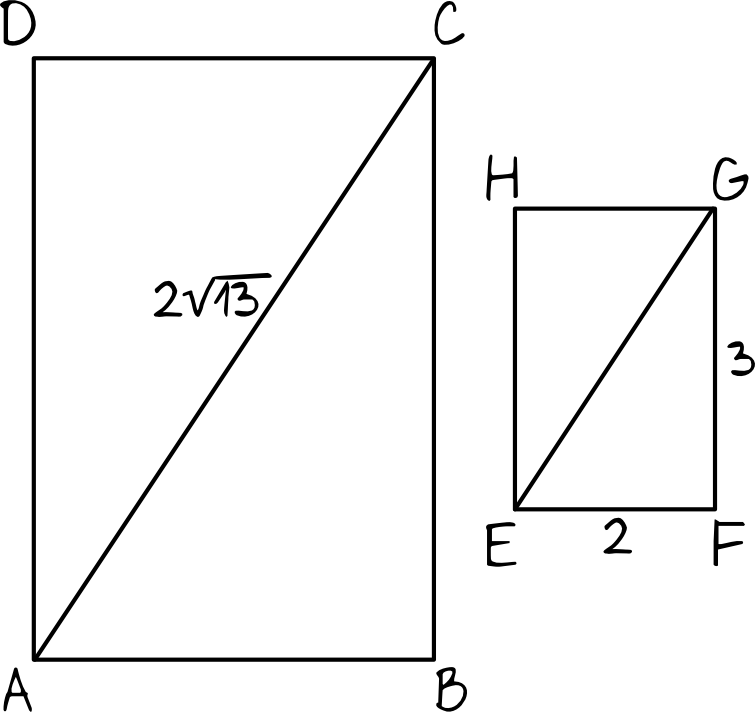
Aby móc porównać oba prostokąty i poznać skalę ich podobieństwa potrzebujemy znać długość przekątnej mniejszego prostokąta \(EFGH\) (patrz rysunek). Obliczymy to oczywiście z Twierdzenia Pitagorasa:
$$2^2+3^2=d^2 \\
4+9=d^2 \\
d^2=13 \\
d=\sqrt{13}$$
Krok 2. Obliczenie obwodu prostokąta \(ABCD\).
Skoro przekątna prostokąta \(ABCD\) jest dwukrotnie większa od przekątnej prostokąta \(EFGH\), to wszystkie boki tego prostokąta są także dwa razy większe. To oznacza, że również i obwód musi być dwukrotnie większy:
Obwód prostokąta \(EFGH\) to \(2\cdot2+2\cdot3=4+6=10\).
Obwód prostokąta \(ABCD\) to \(2\cdot10=20\).
Odpowiedź:
B. \(20\)

