Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczając na rysunku kluczowy trójkąt prostokątny otrzymamy następującą sytuację:
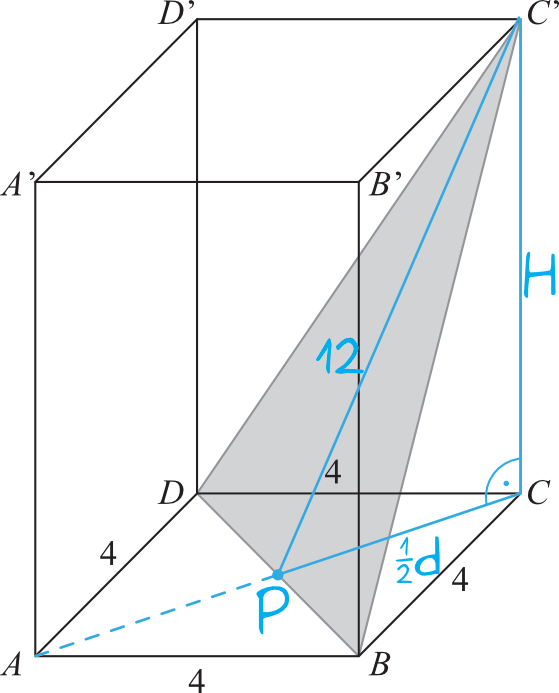
Krok 2. Obliczenie długości przekątnej podstawy.
Graniastosłup jest prawidłowy, czyli w podstawie ma figurę foremną. W tym przypadku będzie to kwadrat. Wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\), zatem skoro bok kwadratu ma długość \(4\), to przekątna będzie mieć długość \(d=4\sqrt{2}\).
Krok 3. Obliczenie długości połowy przekątnej podstawy.
Jak spojrzymy na nasz trójkąt prostokątny zaznaczony na rysunku szkicowym, to zauważymy że do obliczenia długości wysokości bryły potrzebujemy połowy przekątnej podstawy. Skoro tak, to piszemy, że:
$$PC=4\sqrt{2}:2 \\
PC=2\sqrt{2}$$
Krok 4. Obliczenie długości wysokości graniastosłupa.
Patrząc się na zaznaczony niebieski trójkąt prostokątny i korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$(2\sqrt{2})^2+H^2=12^2 \\
4\cdot2+H^2=144 \\
8+H^2=144 \\
H^2=136 \\
H=\sqrt{136} \quad\lor\quad H=-\sqrt{136}$$
Wysokość nie może być ujemna, zatem zostaje nam jedynie \(H=\sqrt{136}\). Aby dopasować się do odpowiedzi, to musimy jeszcze wyłączyć czynnik przed znak pierwiastka, czyli:
$$H=\sqrt{136}=H=\sqrt{4\cdot34}=2\sqrt{34}$$