Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy naszkicować całą sytuację. Na pewno wykres tej funkcji będzie parabolą i to taką, która ma ramiona skierowane do góry (bo współczynnik kierunkowy jest dodatni). Całość będzie wyglądać mniej więcej w ten sposób:
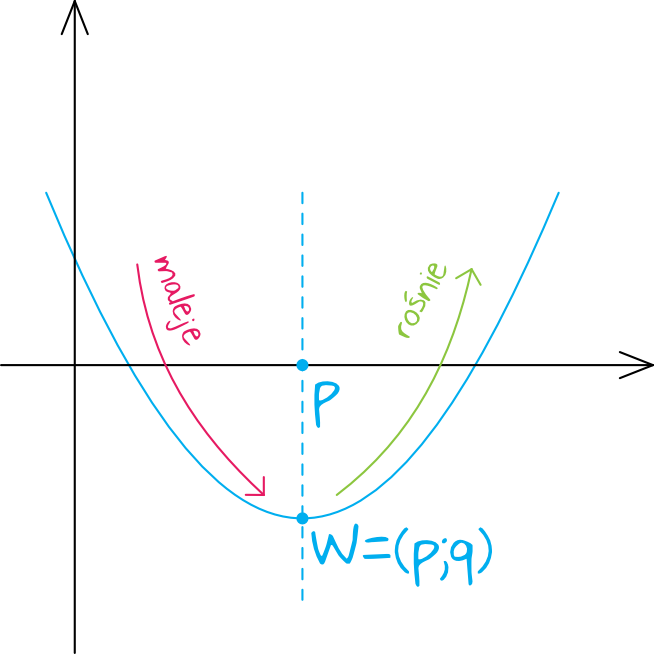
Z rysunku wynika dość wyraźnie, że nasza funkcja będzie malała od minus nieskończoności aż do naszego wierzchołka. To właśnie w wierzchołku się potem odbije i zacznie rosnąć do plus nieskończoności. Wniosek z tego taki, że musimy obliczyć współrzędną iksową naszego wierzchołka (potocznie zapisywaną jako \(p\)).
Krok 2. Obliczenie współrzędnej iksowej wierzchołka.
Współrzędną iksową obliczymy ze wzoru:
$$p=\frac{-b}{2a}$$
W naszym przypadku współczynniki wynoszą odpowiednio: \(a=2,\;b=-4,\;c=5\), zatem:
$$p=\frac{-(-4)}{2\cdot2} \\
p=\frac{4}{4} \\
p=1$$
Krok 3. Zapisanie przedziału.
Wiemy już, że współrzędna iksowa wierzchołka jest równa \(p=1\), zatem funkcja ta maleje w przedziale \(x\in(-\infty,1)\).