Dany jest trapez prostokątny \(ABCD\) o podstawach \(AB\) i \(CD\) oraz wysokości \(AD\). Dwusieczna kąta \(ABC\) przecina ramię \(AD\) w punkcie \(E\) oraz dwusieczną kąta \(BCD\) w punkcie \(F\) (zobacz rysunek).
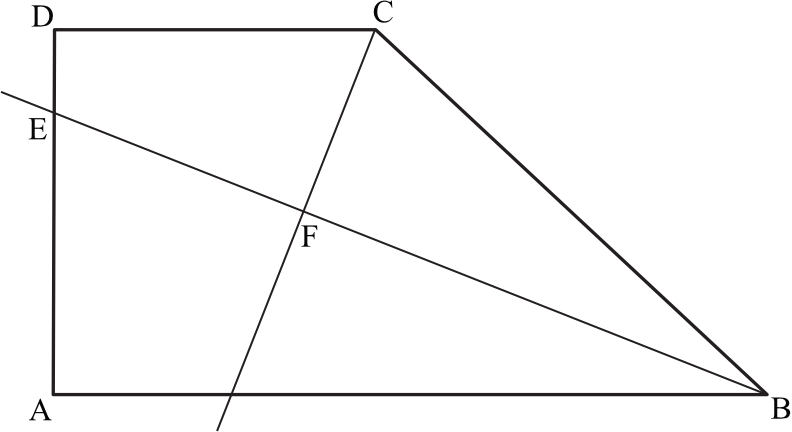
Wykaż, ze w czworokącie \(CDEF\) sumy miar przeciwległych kątów są sobie równe.
Wewnątrz trapezu zostały poprowadzone dwie dwusieczne, więc możemy nanieść na rysunek miary kątów \(α\) oraz \(β\) w następujący sposób:
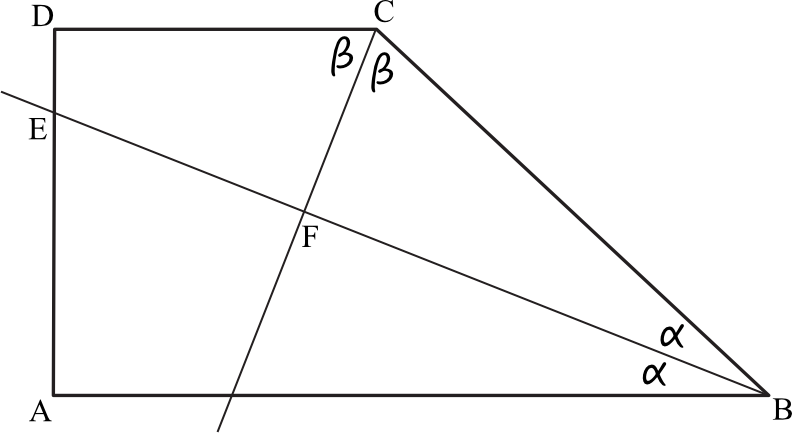
Spójrzmy na trapez \(ABCD\). Jedną z własności trapezu jest to, że suma kątów przy jednym ramieniu jest równa \(180°\). To oznacza, że:
$$|\sphericalangle ABC|+|\sphericalangle BCD|=180° \\
2α+2β=180° \quad\bigg/:2 \\
α+β=90°$$
Gdybyśmy nie pamiętali o tym, że suma miar przy jednym ramieniu trapezu jest równa \(180°\), to mogliśmy od \(360°\) odliczyć dwa kąty proste \(DAB\) oraz \(CDA\) i także doszlibyśmy do wniosku, że \(|\sphericalangle ABC|+|\sphericalangle BCD|=180°\).
Zacznijmy od kąta \(BFC\). Jego miarę możemy oznaczyć jako \(180°-(α+β)\), bo suma kątów w trójkącie \(BFC\) musi być równa \(180°\). Wiedząc, że \(α+β=90°\) okazuje się, że \(|\sphericalangle BFC|=90°\).
Kąt \(EFC\) jest przyległy do kąta \(BFC\), a więc jego miara jest równa \(180°-90°=90°\).
Spójrzmy na czworokąt \(CDEF\).
Skoro \(|\sphericalangle EFC|=90°\) oraz \(|\sphericalangle CDE|=90°\), to suma miar pierwszej pary kątów leżących naprzeciwko siebie jest równa \(180°\).
Suma kątów w czworokącie musi być równa \(360°\), więc to oznacza, że suma kątów w drugiej parze kątów przeciwległych jest równa:
$$|\sphericalangle FCD|+|\sphericalangle DEF|=360°-180°=180°$$
Suma miar przeciwległych kątów czworokąta \(CDEF\) jest więc jednakowa, co należało udowodnić.
Udowodniono wykorzystując własności trapezów i kątów.

