Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W sześciokącie foremnym mamy trzy dłuższe przekątne równej miary, które przecinają się w połowie swojej długości. Wiemy, że każda taka dłuższa przekątna ma miarę \(2\sqrt{2}\), zatem cała sytuacja będzie więc wyglądać mniej więcej w ten sposób:
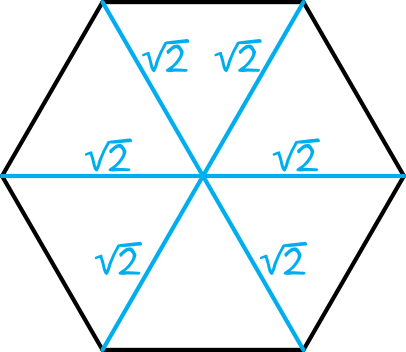
Krok 2. Obliczenie pola powierzchni pojedynczego trójkąta.
Powstało nam sześć trójkątów równobocznych, każdy o boku \(a=\sqrt{2}\). Korzystając ze wzoru na pole trójkąta równobocznego możemy obliczyć, że pole każdego z tych pojedynczych trójkątów jest równe:
$$P=\frac{a^2\sqrt{3}}{4} \\
P=\frac{(\sqrt{2})^2\sqrt{3}}{4} \\
P=\frac{2\sqrt{3}}{4} \\
P=\frac{\sqrt{3}}{2}$$
Krok 3. Obliczenie pola sześciokąta.
Sześciokąt składa się z sześciu takich trójkątów równobocznych, zatem jego pole powierzchni będzie równe:
$$P=6\cdot\frac{\sqrt{3}}{2} \\
P=3\sqrt{3}$$