Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować sobie tę sytuację w układzie współrzędnych.
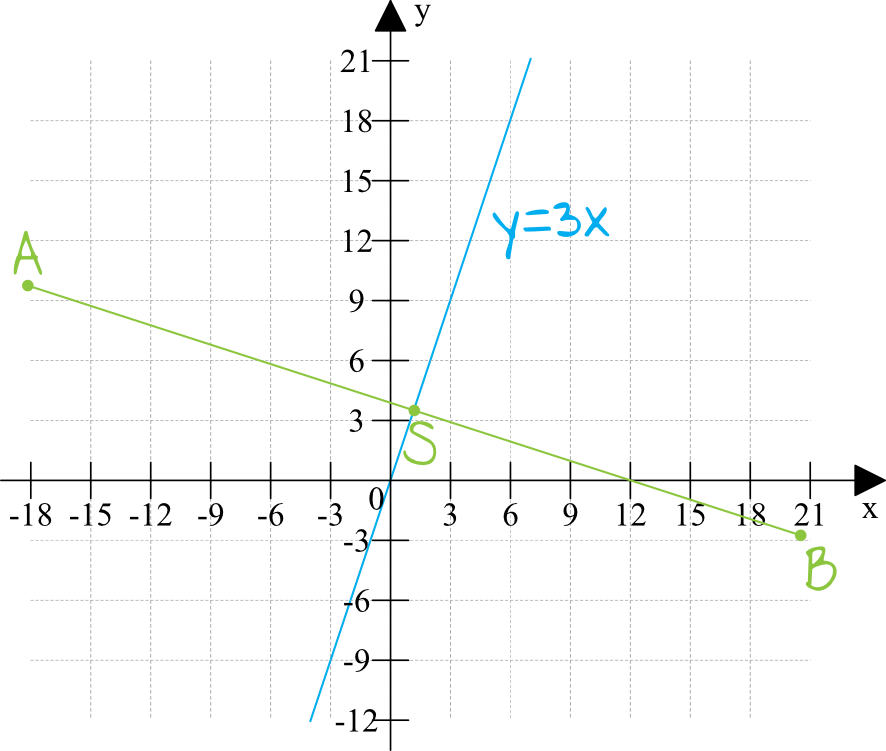
Krok 2. Ustalenie współczynnika kierunkowego \(a\) prostej \(AB\).
Symetralna odcinka to nic innego jak prosta prostopadła, która musi przechodzić przez środek odcinka. Skoro to ma być prosta prostopadła do prostej przechodzącej \(AB\) i wiemy, że ta symetralna wyraża się równaniem \(y=3x\), to możemy wyznaczyć współczynnik kierunkowy \(a\) naszej prostej przechodzącej przez punkty \(AB\).
Iloczyn współczynników kierunkowych prostych prostopadłych ma być równy \(-1\), zatem skoro symetralna ma \(a=3\), to prosta \(AB\) musi mieć ten współczynnik równy \(a=-\frac{1}{3}\).
To też oznacza, że nasza prosta \(AB\) musi wyrażać się wzorem:
$$y=-\frac{1}{3}x+b$$
Krok 3. Wyznaczenie równania prostej \(AB\).
Do pełnego wzoru prostej \(AB\) brakuje nam znajomości współczynnika \(b\). Wiemy, że prosta przechodzi przez punkt \(A=(-18,10)\) i podstawiając te współrzędne do wyznaczonej przed chwilą postaci \(y=-\frac{1}{3}x+b\) wyznaczymy brakujący współczynnik \(b\). Zatem:
$$10=-\frac{1}{3}\cdot(-18)+b \\
10=6+b \\
b=4$$
To oznacza, że nasza prosta \(AB\) wyraża się równaniem:
$$y=-\frac{1}{3}x+4$$
Krok 4. Wyznaczenie środka odcinka \(AB\).
Prosta AB oraz symetralna przecinają się w punkcie, który jest środkiem odcinka \(AB\) (jest to własność symetralnej). Z geometrycznej interpretacji układu równań wiemy, że rozwiązując układ równań składający się z dwóch prostych wyznaczymy współrzędne punktu ich przecięcia, czyli w naszym przypadku współrzędne środka odcinka \(AB\). Zatem:
$$\begin{cases}
y=3x \\
y=-\frac{1}{3}x+4
\end{cases}$$
Korzystając z metody podstawiania mamy:
$$3x=-\frac{1}{3}x+4 \quad\bigg/\cdot3 \\
9x=-x+12 \\
10x=12 \\
x=\frac{12}{10}=\frac{6}{5}$$
Znając wartość iksa możemy teraz obliczyć współrzędną igrekową, korzystając z dowolnego równania np. \(y=3x\), zatem:
$$y=3\cdot\frac{6}{5} \\
y=\frac{18}{5}$$
To oznacza, że współrzędne środka odcinka \(AB\) to:
$$S=\left(\frac{6}{5}; \frac{18}{5}\right)$$
Krok 5. Wyznaczenie współrzędnych punktu \(B\).
Znamy współrzędne punktu \(A\), znamy współrzędne punktu \(S\) (czyli środka odcinka), zatem możemy bez przeszkód obliczyć współrzędne punktu \(B\), korzystając ze wzoru:
$$S=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right)$$
Dla przejrzystości obliczeń możemy policzyć każdą ze współrzędnych oddzielnie:
$$x_{S}=\frac{x_{A}+x_{B}}{2} \\
\frac{6}{5}=\frac{-18+x_{B}}{2} \\
\frac{12}{5}=-18+x_{B} \\
\frac{12}{5}=-\frac{90}{5}+x_{B} \\
x_{B}=\frac{102}{5}=20\frac{2}{5} \\
\quad \\
\text{oraz} \\
\quad \\
y_{S}=\frac{y_{A}+y_{B}}{2} \\
\frac{18}{5}=\frac{10+y_{B}}{2} \\
\frac{36}{5}=10+y_{B} \\
\frac{36}{5}=\frac{50}{5}+y_{B} \\
y_{B}=-\frac{14}{5}=-2\frac{4}{5}$$
To oznacza, że \(B=(20\frac{2}{5}; -2\frac{4}{5})\).