Do tej pory potrafiliśmy wyznaczać długości odcinków w układzie współrzędnych tylko w dwóch przypadkach – kiedy odcinek był równoległy do osi iksów lub równoległy do osi igreków. Twierdzenie Pitagorasa pozwala nam wyznaczyć długość dowolnie ułożonego odcinka i właśnie tym zajmiemy się w tym zagadnieniu.
Spójrzmy na poniższy rysunek:
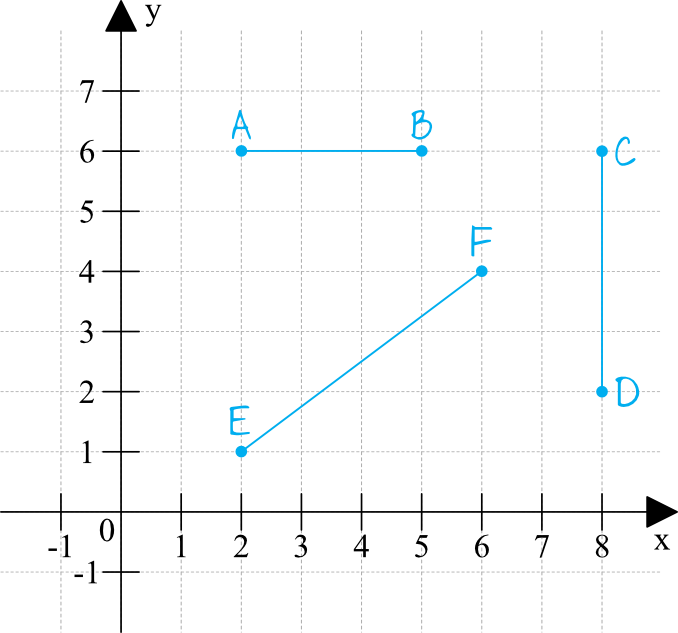
Aby wyznaczyć długość odcinka \(AB\) odczytujemy z osi iksów odpowiednie współrzędne i zazwyczaj po kratkach obliczamy jaka jest długość tego boku. Podobnie jest w przypadku odcinka \(CD\) – tutaj także odczytujemy współrzędne (tym razem z osi igreków) no i obliczamy jaka jest długość tego boku. Jak jednak obliczyć długość odcinka \(EF\)? Jeżeli wyobrazimy sobie, że odcinek \(EF\) jest przeciwprostokątną pewnego trójkąta prostokątnego, to będziemy mogli skorzystać z Twierdzenia Pitagorasa, spójrzmy na rysunek:
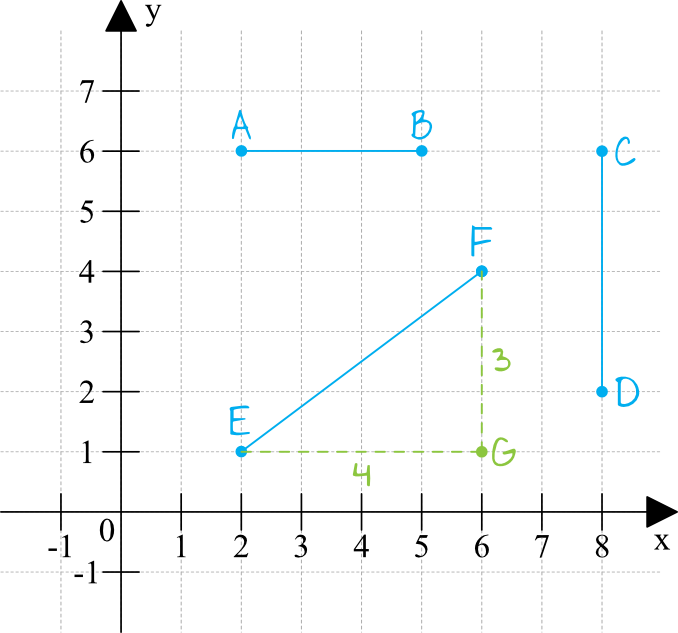
Dorysowaliśmy sobie odcinki \(EG\) oraz \(FG\), które są tak naprawdę przyprostokątnymi trójkąta prostokątnego \(EFG\). Potrafimy też podać długości tych odcinków, licząc po kratkach tak jak boki \(AB\) oraz \(CD\). Dzięki tej obserwacji możemy wyznaczyć długość przeciwprostokątnej, czyli interesującego nas odcinka \(EF\):
$$a^2+b^2=c^2 \\
|EG|^2+|FG|^2=|EF|^2 \\
3^2+4^2=|EF|^2 \\
9+16=|EF|^2 \\
|EF|^2=25 \\
|EF|=5$$
W ten oto sprytny sposób wiemy, że odcinek \(EF\) ma długość \(5\).
Spójrzmy na przykładowe zadanie z tego zagadnienia:
Zacznijmy od zaznaczenia tych dwóch punktów w układzie współrzędnych:
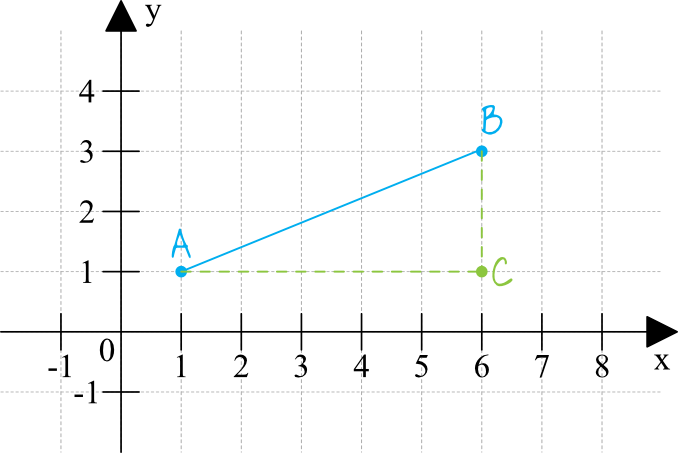
Aby obliczyć długość odcinka \(AB\) posłużymy się Twierdzeniem Pitagorasa na dorysowanym trójkącie \(ABC\). Możemy zatem zapisać, że:
$$|AC|^2+|BC|^2=|AB|^2 \\
5^2+2^2=|AB|^2 \\
25+4=|AB|^2 \\
|AB|=\sqrt{29}$$

było bardzo pomocne
Fajne pomocne! Dziękuję i polecam