Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Dla lepszego zobrazowania sytuacji, narysujmy sobie układ współrzędnych z zaznaczonymi informacjami z treści zadania:
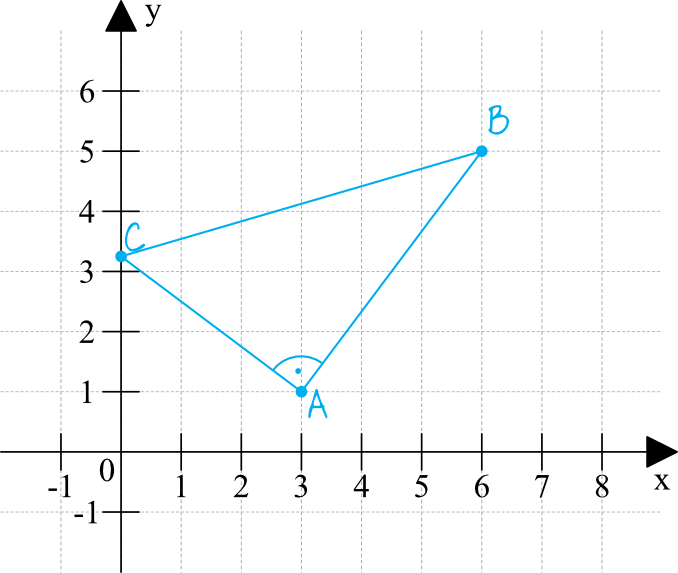
Z rysunku jasno wynika, że kluczem do sukcesu będzie najpierw poznanie równania prostej \(AB\), a następnie odszukanie prostej prostopadłej, która przechodzi przez punkt \(C\). To właśnie pozwoli nam na wyznaczenie współrzędnych punktu \(C\).
Krok 2. Wyznaczenie współczynnika kierunkowego \(a\) prostej \(AB\).
Znając współrzędne punktów \(A\) oraz \(B\), możemy bez problemu wyznaczyć wzór prostej \(AB\), która przez te punkty przechodzi. W tym celu możemy skorzystać z bardzo rozbudowanego wzoru z tablic lub z metody układu równań. Jednak nam tak naprawdę wystarczy poznanie współczynnika kierunkowego \(a\) tej prostej, bo to właśnie jego potrzebujemy do dalszego rozwiązywania. Możemy więc skorzystać ze wzoru na współczynnik \(a\), czyli:
$$a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}} \\
a=\frac{5-1}{6-3} \\
a=\frac{4}{3}$$
Oczywiście jeśli nie pamiętamy o tym wzorze, to możemy wyznaczyć ten współczynnik \(a\) w standardowy sposób, czyli w trakcie wyznaczania równania prostej. W tym celu do równania prostej \(y=ax+b\) musimy podstawić najpierw współrzędne punktu \(A\), a potem współrzędne punktu \(B\), otrzymując takie oto dwa równania:
\begin{cases}
1=3a+b \\
5=6a+b
\end{cases}
Odejmując te równania stronami otrzymamy:
$$-4=-3a \\
a=\frac{4}{3}$$
Współczynnika \(b\) nie musimy już wyznaczać, wystarczy nam informacja, że \(a=\frac{4}{3}\).
Krok 3. Wyznaczenie równania prostej \(AC\).
Prosta \(AC\) musi być prostopadła do \(AB\). Z własności prostych wiemy, że aby tak się stało, to iloczyn współczynników kierunkowych \(a\) musi być równy \(-1\). Skoro prosta \(AB\) ma ten współczynnik równy \(a=\frac{4}{3}\), to prosta \(AC\) będzie mieć \(a=-\frac{3}{4}\), bo \(-\frac{3}{4}\cdot\frac{4}{3}=-1\).
To oznacza, że prosta \(AC\) wyraża się równaniem \(y=-\frac{3}{4}x+b\). Musimy jeszcze odnaleźć brakujący współczynnik \(b\) tej prostej, a dokonamy tego, podstawiając do tego równania współrzędne znanego nam punktu, który do tej prostej należy, czyli w tym przypadku punktu \(A\), zatem:
$$y=-\frac{3}{4}x+b \\
1=-\frac{3}{4}\cdot3+b \\
1=-\frac{9}{4}+b \\
b=3\frac{1}{4}$$
To oznacza, że prosta \(AC\) wyraża się równaniem \(y=-\frac{3}{4}x+3\frac{1}{4}\).
Krok 4. Ustalenie współrzędnych punktu \(C\).
Punkt \(C\) leży na osi \(Oy\), zatem na pewno współrzędna \(x=0\). Współrzędną \(y\) możemy w takim razie odczytać wprost z równania prostej \(AC\) - jest ona równa współczynnikowi \(b\), czyli jest równa \(3\frac{1}{4}\). Jeśli o tej własności nie pamiętamy, to możemy po prostu podstawić \(x=0\) do wzoru prostej \(y=-\frac{3}{4}x+3\frac{1}{4}\). Otrzymamy wtedy:
$$y=-\frac{3}{4}\cdot0+3\frac{1}{4} \\
y=0+3\frac{1}{4} \\
y=3\frac{1}{4}$$
To oznacza, że poszukiwane współrzędne to \(C=\left(0;3\frac{1}{4}\right)\).