Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanieśmy na rysunek informacje z treści zadania.
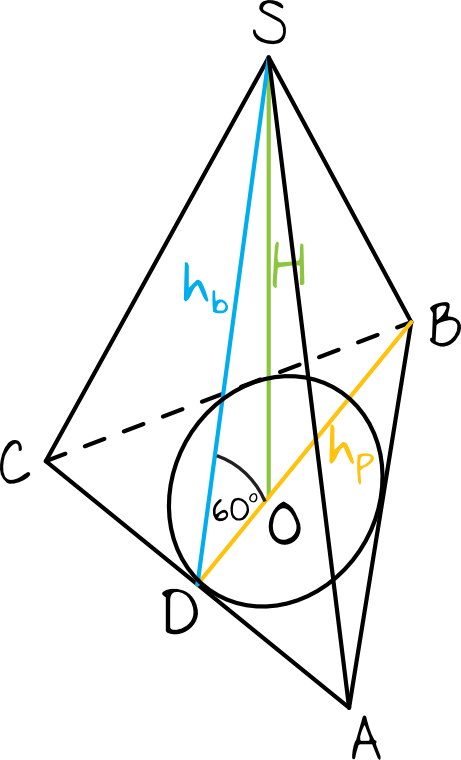
Krok 2. Obliczenie wysokości trójkąta znajdującego się w podstawie.
Z własności okręgów wpisanych w trójkąt równoboczny wiemy, że długość promienia okręgu jest równa \(\frac{1}{3}\) wysokości takiego trójkąta, zatem:
$$h_{p}=3\cdot6=18$$
Krok 3. Obliczenie długości boku trójkąta znajdującego się w podstawie.
W podstawie znajduje się trójkąt równoboczny o wysokości \(h_{p}=18\), zatem jego długość boku będzie równa:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
18=\frac{a\sqrt{3}}{2} \\
36=a\sqrt{3} \\
a=\frac{36}{\sqrt{3}} \\
a=\frac{36\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \\
a=\frac{36\sqrt{3}}{3} \\
a=12\sqrt{3}$$
Krok 4. Obliczenie wysokości ostrosłupa.
Spójrzmy na trójkąt \(SOD\). Wiemy, że podstawa tego trójkąta (czyli odcinek \(DO\) będący promieniem okręgu) ma długość \(r=6\). Korzystając z funkcji trygonometrycznych (a konkretnie z tangensa) możemy zapisać, że:
$$tg60°=\frac{H}{|DO|} \\
\sqrt{3}=\frac{H}{6} \\
H=6\sqrt{3}$$
Krok 5. Obliczenie wysokości ściany bocznej.
Ponownie spoglądamy na trójkąt \(SOD\). Do obliczenia pola powierzchni bocznej potrzebujemy znać długość wysokości ściany bocznej, a tę możemy obliczyć albo z Twierdzenia Pitagorasa (bo wiemy już, że przyprostokątne mają długości \(|DO|=6\) oraz \(H=6\sqrt{3}\)), albo po prostu z cosinusa:
$$cos60°=\frac{|DO|}{h_{b}} \\
\frac{1}{2}=\frac{6}{h_{b}} \\
\frac{1}{2}h_{b}=6 \\
h_{b}=12$$
Krok 6. Obliczenie objętości ostrosłupa.
Mamy już komplet informacji na temat naszego ostrosłupa, bo wiemy że \(a=12\sqrt{3}\) oraz \(H=6\sqrt{3}\), więc możemy przystąpić do obliczenia objętości, korzystając ze wzoru:
$$V=\frac{1}{3}\cdot P_{p}\cdot H \\
V=\frac{1}{3}\cdot\frac{a^2\sqrt{3}}{4}\cdot H \\
V=\frac{1}{3}\cdot\frac{(12\sqrt{3})^2\sqrt{3}}{4}\cdot6\sqrt{3} \\
V=\frac{1}{3}\cdot\frac{432\sqrt{3}}{4}\cdot6\sqrt{3} \\
V=\frac{1}{3}\cdot108\sqrt{3}\cdot6\sqrt{3} \\
V=36\sqrt{3}\cdot6\sqrt{3} \\
V=216\cdot3 \\
V=648$$
Krok 7. Obliczenie pola powierzchni bocznej.
W powierzchni bocznej mamy trzy trójkąty o podstawie \(a=12\sqrt{3}\) oraz wysokości \(h_{b}=12\), zatem:
$$P_{b}=3\cdot\frac{1}{2}\cdot a\cdot h_{b} \\
P_{b}=3\cdot\frac{1}{2}\cdot12\sqrt{3}\cdot12 \\
P_{b}=3\cdot6\sqrt{3}\cdot12 \\
P_{b}=216\sqrt{3}$$