Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Jeżeli w przekroju osiowym walca mamy kwadrat, to sytuacja będzie wyglądać w ten oto sposób:
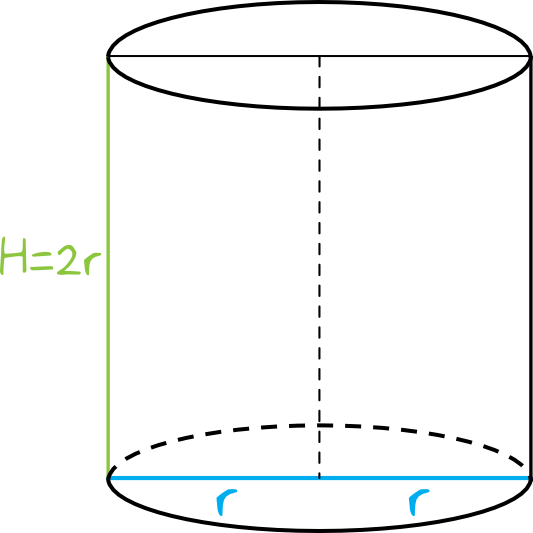
Z rysunku wynika, że wysokość \(H\) będzie równa długości \(2r\) i to będzie dla nas za chwilę klucz do rozwiązania tego zadania.
Krok 2. Obliczenie pola powierzchni bocznej.
Pole powierzchni bocznej obliczymy ze wzoru:
$$P_{b}=2πrH$$
Podstawiając pod \(H\) wartość \(2r\) otrzymamy:
$$P_{b}=2πr\cdot2r \\
P_{b}=4πr^2$$
Krok 3. Obliczenie pola powierzchni całkowitej.
Na pole powierzchni całkowitej składa się pole dwóch podstaw oraz pole powierzchni bocznej:
$$P_{c}=2P_{p}+P_{b}$$
W podstawie (zarówno dolnej jak i górnej) znajduje się koło o promieniu \(r\), zatem korzystając ze wzoru na pole koła możemy zapisać, że \(P_{p}=πr^2\). Podstawiając tę wartość oraz wyznaczoną przed chwilą powierzchnię boczną otrzymamy:
$$P_{c}=2\cdotπr^2+4πr^2 \\
P_{c}=6πr^2$$
Takiego konkretnego wyniku w proponowanych odpowiedziach nie mamy, ale skoro \(P_{b}=4πr^2\), to możemy zapisać, że:
$$P_{c}=\frac{3}{2}\cdot4πr^2 \\
P_{c}=\frac{3}{2}\cdot P_{b}$$