Rozwiązanie
Krok 1. Wyznaczenie współrzędnych wierzchołka paraboli.
Funkcja kwadratowa zapisana jest w postaci kanonicznej \(f(x)=a(x-p)^2+q\). Z takiej postaci możemy wprost odczytać współrzędne wierzchołka paraboli \(W=(p;q)\), czyli: \(p=1\) oraz \(q=3\).
Krok 2. Wyznaczenie przedziału w którym funkcja jest rosnąca.
Współczynnik \(a\) tej funkcji jest ujemny, więc ramiona paraboli będą skierowane do dołu. Sytuacja z treści zadania wygląda więc następująco:
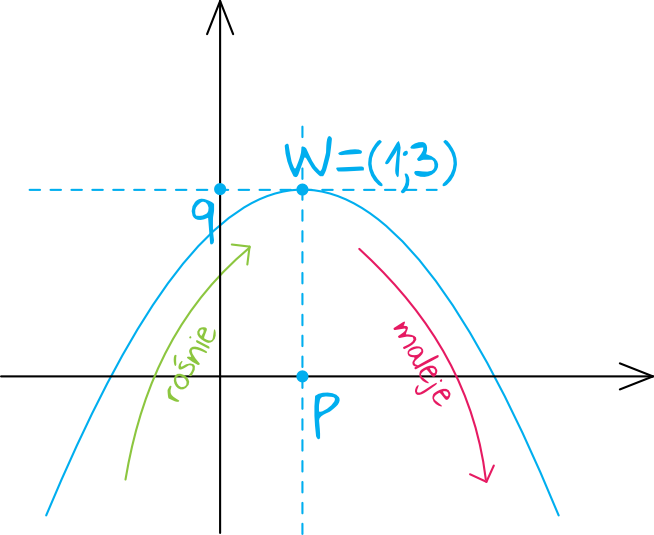
Funkcja kwadratowa zawsze jest rosnąca od wierzchołka lub do wierzchołka (w zależności od ułożenia ramion paraboli). Z rysunku jasno wynika, że w takim razie funkcja jest rosnąca w przedziale \((-\infty,1\rangle\).