Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Oznaczmy na rysunku kąt nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy, tak aby wiedzieć, co tak naprawdę musimy policzyć i przy okazji wprowadźmy proste oznaczenia niektórych odcinków:
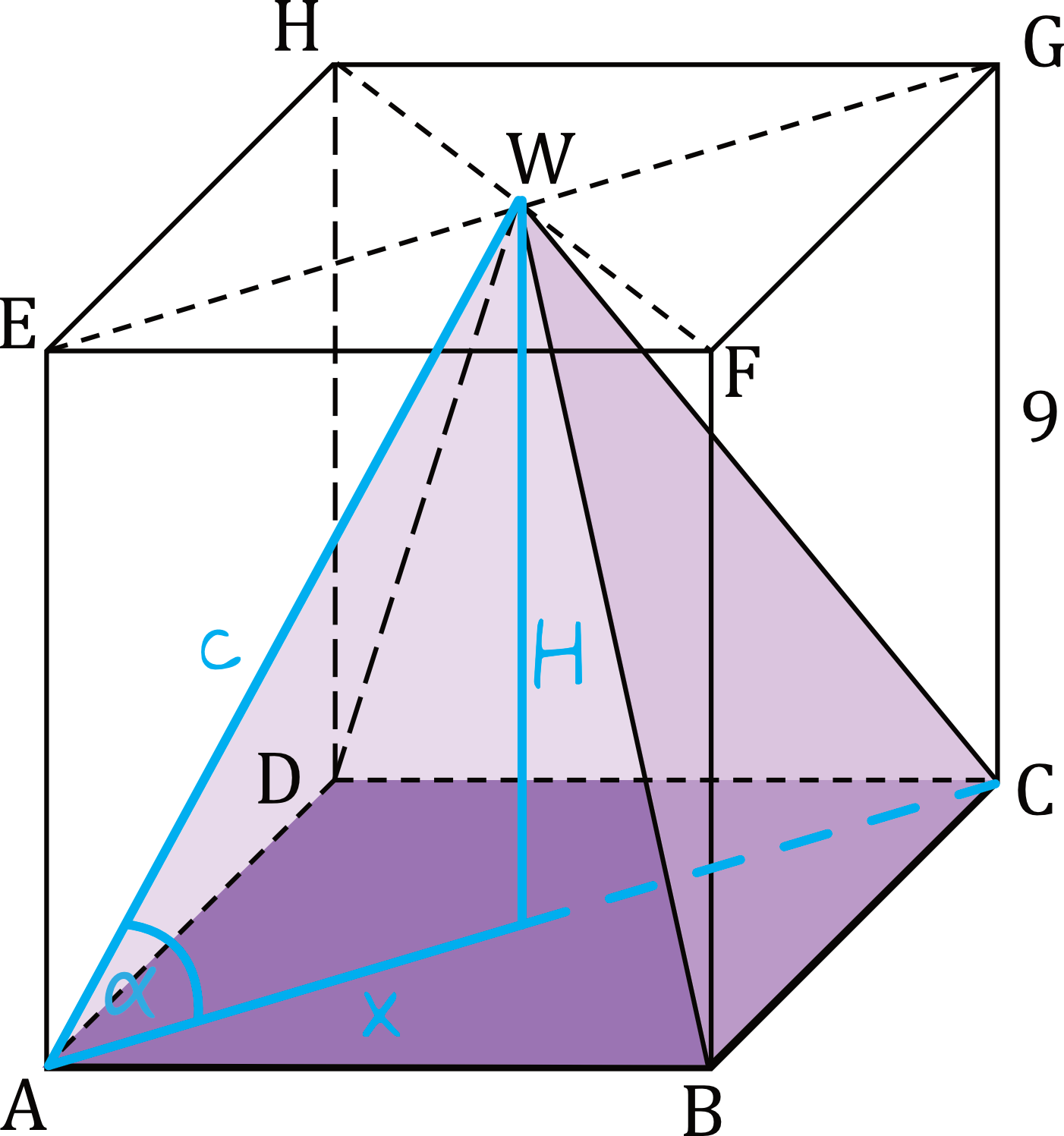
Widzimy, że na rysunku powstał nam kluczowy trójkąt prostokątny, na który składa się połowa długości przekątnej kwadratu, wysokość ostrosłupa oraz krawędź boczna. I to właśnie z tego trójkąta obliczymy za chwilę potrzebne długości (do wyznaczenia cosinusa będziemy potrzebować połowy przekątnej podstawy oraz krawędź boczną).
Krok 2. Obliczenie długości połowy przekątnej podstawy.
W podstawie ostrosłupa znajduje się kwadrat. Przekątna kwadratu o boku \(a\) ma zawsze długość \(a\sqrt{2}\), więc w naszym przypadku cała przekątna kwadratu ma długość:
$$d=9\sqrt{2}$$
Do obliczenia cosinusa potrzebujemy połowy przekątnej (oznaczonej jako \(x\)), zatem:
$$x=\frac{9\sqrt{2}}{2}$$
Krok 3. Obliczenie długości krawędzi bocznej.
Krawędź boczna jest jednocześnie przeciwprostokątną naszego trójkąta \(AOW\). W tym trójkącie znamy już długości dwóch boków, ponieważ \(x=\frac{9\sqrt{2}}{2}\) oraz \(H=9\). Skoro tak, to korzystając z twierdzenia Pitagorasa, otrzymamy:
$$x^2+H^2=c^2 \\
\left(\frac{9\sqrt{2}}{2}\right)^2+9^2=c^2 \\
\frac{81\cdot2}{4}+81=c^2 \\
\frac{162}{4}+81=c^2$$
Tu na chwilę się zatrzymamy - mamy tutaj dość nietypową sytuację, ponieważ jeśli będziemy kontynuowali dodawanie w standardowy sposób, to otrzymamy równanie \(c^2=121,5\) i dość trudno będzie tutaj uzyskać "ładny" zapis. Z tego też względu, lepiej byłoby dokonać takiego przekształcenia:
$$\frac{81\cdot2}{4}+81=c^2 \\
\frac{81\cdot2}{4}+\frac{81\cdot4}{4}=c^2 \\
c^2=\frac{81\cdot6}{4} \\
c=\sqrt{\frac{81\cdot6}{4}} \quad\lor\quad c=-\sqrt{\frac{81\cdot6}{4}}$$
Ujemny wynik oczywiście odrzucamy, ponieważ długość krawędzi jest na pewno dodatnia. Stąd też zostaje nam \(c=\sqrt{\frac{81\cdot6}{4}}\), co możemy rozpisać w następujący sposób:
$$c=\sqrt{\frac{81\cdot6}{4}} \\
c=\frac{9\sqrt{6}}{2}$$
Krok 4. Obliczenie cosinusa kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Mamy już komplet danych, więc możemy przystąpić do obliczenia cosinusa. Cosinus odpowiada za stosunek długości przyprostokątnej leżącej przy kącie względem przeciwprostokątnej, zatem:
$$cos\alpha=\frac{\frac{9\sqrt{2}}{2}}{\frac{9\sqrt{6}}{2}} \\
cos\alpha=\frac{9\sqrt{2}}{2}:\frac{9\sqrt{6}}{2} \\
cos\alpha=\frac{9\sqrt{2}}{2}\cdot\frac{2}{9\sqrt{6}} \\
cos\alpha=\frac{\sqrt{2}}{\sqrt{6}} \\
cos\alpha=\frac{\sqrt{2}}{\sqrt{2}\cdot\sqrt{3}} \\
cos\alpha=\frac{1}{\sqrt{3}}$$
Otrzymany wynik jest już poprawny, ale dobrze byłoby się jeszcze pozbyć niewymierności z mianownika. W tym celu trzeba byłoby pomnożyć licznik oraz mianownik ułamka przez \(\sqrt{3}\), otrzymując:
$$cos\alpha=\frac{1\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \\
cos\alpha=\frac{\sqrt{3}}{3}$$
Dzięki pomogło na lekcji